Il calcolo dei limiti si svolge attraverso quella che viene definita algebra dei limiti. Si tratta cioè di semplificare al massimo ogni operazione, così da ridurla ad un insieme di somme algebriche, prodotti o rapporti.
Una volta note la definizione di limite di una funzione, generalmente considerate più difficili, il vero e proprio calcolo del limite si effettua in maniera più semplice e ricorrendo a delle regole elementari.
Regole calcolo limiti
Siano date le generiche funzioni f(x) e g(x), con x0 punto di accumulazione sia di f che di g entrambe continue in x0. Allora per la risoluzione dei limiti possiamo prendere come riferimento le proprietà che seguono.
Di seguito troverai un piccolo paragrafo che ti spiega in maniera molto semplice come risolvere i limiti con le operazioni principali.
Calcolo del limite della somma
Il limite della somma è uguale alla somma dei limiti
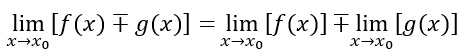
Questo vuol dire che possiamo semplicemente spezzare la somma/differenza ed applicare ad ogni elemento il limite.
Calcolo del limite del prodotto
Per una costante
Il limite del prodotto di una funzione f(x) per una costante k, è pari alla costante per il limite della funzione.
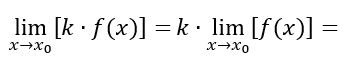
In parole povere qualsiasi costante (cioè numero) può andare fuori dall’operazione di limite.
Tra due funzioni
Il limite del prodotto/rapporto di due funzioni, è pari al prodotto/rapporto dei limiti delle funzioni.
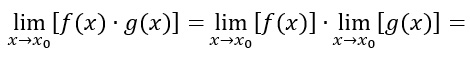
Così come visto nella prima regola, anche il prodotto e il rapporto, come la somma e la differenza, possono essere spezzati in due limiti differenti.
Come applicare le regole di calcolo dei limiti
La regola della sostituzione
Vedremo nelle lezioni successive che la risoluzione limiti che darà maggiori problemi riguarderà i casi indeterminati, ovvero quei casi in cui arrivare ad una soluzione non sarà così immediato.
I primi esercizi svolti che vedremo, però, possono essere risolti semplicemente andando a sostituire il punto di accumulazione all’interno della funzione.
ESEMPIO 1
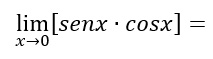
Dobbiamo in questo caso determinare il limite del prodotto della funzione seno di x e della funzione coseno di x. Applichiamo la regola sulla moltiplicazione, per cui possiamo separare i due fattori:
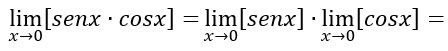
A questo punto possiamo sostituire 0 al posto della x, così da ottenere:
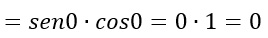
In questo primo esempio abbiamo svolto il calcolo del limite riportando ogni passaggi. E’ facile rendersi conto, però, che il secondo step – ovvero l’applicazione della regola della moltiplicazione – può anche essere saltata.
Possiamo infatti direttamente sostituire lo zero al posto della x, così da arrivare rapidamente alla soluzione dell’esercizio.
DOMANDA DEGLI STUDENTI:
E’ possibile quindi calcolare i limiti con la calcolatrice?
RISPOSTA:
Si, in questa prima fase la calcolatrice può esserti molto d’aiuto per eseguire i calcoli di sostituzione nella funzione data.
ESERCIZIO 2
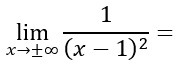
In questo secondo esercizio svolto, abbiamo aumentato il livello di difficoltà, ma la sostanza non cambia. Basta applicare l’algebra dei limiti, senza ricorrere a teoremi o regole: semplicemente sostituiamo infinito all’interno della funzione fratta presentata.
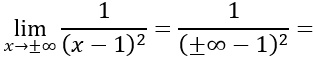
A questo punto non resta che fare le somme: quanto fa infinito meno uno? Un numero grandissimo meno un numero piccolo resta grandissimo, per cui il risultato è infinito.
NB: Ricordati che un numero sommato/sottratto ad infinito può essere trascurato. Per cui il risultato sarà sempre infinito.
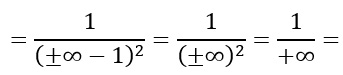
Poiché anche infinito al quadrato è uguale a infinito, non ci resta da risolvere che 1 fratto infinito. Quanto fa? Immagina di fare la divisione tra un numero molto piccolo (1) e uno molto grande (infinito). Il risultato è prossimo allo zero!
NON CI CREDI? Prova a fare sulla tua calcolatrice 1 diviso 999999 (un numero molto grande come infinito). Vedrai che il risultato è zero virgola zero zero zero …. cioè il risultato è zero.
Il risultato finale del calcolo del limite è quindi 0.
ESERCIZIO 3
La funzione di cui calcolare il limite è la stessa, ma il punto di accumulazione questa volta è 0. Vediamo cosa cambia…
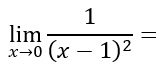
Anche in questo caso procediamo con lo stesso metodo della sostituzione visto sopra. Quindi al posto della x mettiamo lo zero.
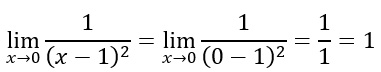
ESERCIZIO 4
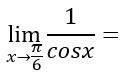
Sostituiamo quindi pi greco fratto sei all’interno della funzione, così da ottenere:
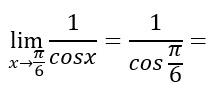
A questo punto basta calcolare il coseno di 30 gradi per terminare l’esercizio:
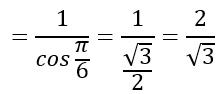
ESERCIZIO 5
In questo esempio vedremo come si fa il calcolo limite destro e sinistro.
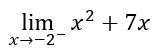
Come puoi notare è espresso il limite per x che tende a -2 con l’apice meno. Significa che è il limite sinistro. Come prima cosa andiamo a sostituire al posto della x il valore indicato.
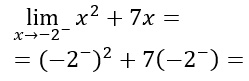
Ricordati che “meno due meno” puoi rappresentarlo sulla calcolatrice scrivendo -2,0001. Completiamo le operazioni sui limiti svolgendo gli ultimi calcoli:
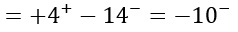
Conclusioni
Abbiamo visto in questa lezione come fare il calcolo dei limiti attraverso l’uso dell’algebra e di alcune regole che, alla fine, si basano su una semplice sostituzione. In base a quello che hai letto oggi, prova a guardare questa traccia:
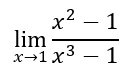
Sostituendo 1 al numeratore e al denominatore, il risultato sarà 0 fratto 0. Non è un risultato accettabile (se provi sulla tua calcolatrice a fare 0/0 ti darà errore). Si tratta infatti di una forma indeterminata che andrà risolta con un metodo differente. Vedremo che alcuni di questi casi si potranno risolvere solo con l’uso di limiti notevoli.
Vuoi scoprire come risolvere questo tipo di esercizio? Vai alla lezione sulle forme indeterminate dei limiti.