L’asintoto orizzontale è una retta orizzontale a cui la funzione tende verso infinito. Va a rappresentare l’andamento del grafico tendenziale di una curva nei suoi estremi più infinito o meno infinito.
Se ci hai capito poco, non preoccuparti. In questa lezione vedremo in maniera più approfondita e semplificata che cos’è l’asintoto orizzontale, con esempi ed esercizi svolti.
Come si trova l’asintoto orizzontale
Nella lezione dedicata all’asintoto verticale abbiamo visto come anche dalla definizione dello studio del dominio di una funzione è possibile ottenere preziosi informazioni. Con l’asintoto verticale invece è necessario calcolare il limite per andare a stabilire il comportamento della funzione nei suoi estremi.
Definizione di asintoto orizzontale destro
Una condizione fondamentale affinché una funzione abbia un asintoto orizzontale, è che questa sia illimitata sia superiormente che inferiormente. Che significa? Che la funzione deve tendere ad un numero finito quando l’ascissa va a +∞ e -∞. Dal punto di vista matematico, questo si traduce con l’espressione:
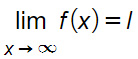
Cioè il limite della funzione per x che tende a più infinito è uguale a l. Allora l’equazione della retta y=l è per definizione un asintoto orizzontale destro.
Vediamo graficamente invece questo cosa significa:
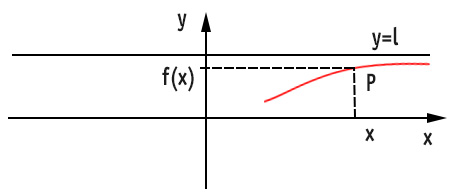
Come puoi osservare dalla figura, data la funzione segnata in rossa, esaminiamo il punto P, di coordinate x e f(x). Man mano che l’ascissa di P si avvicina a +∞, la y si avvicinerà sempre di più alla y della retta asintoto orizzontale.
Definizione di asintoto orizzontale sinistro
Il caso è analogo per il limite che tende a meno infinito. In questo caso si parla di asintoto orizzontale sinistro. Dal punto di vista matematico questo si può scrivere come:
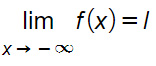
Cioè il limite della funzione, per x che tende a meno infinito è uguale a l. In questo caso la retta di equazione y=l è per definizione un asintoto orizzontale sinistro.
Vediamo dal punto di vista grafico che cosa significa questa definizione:
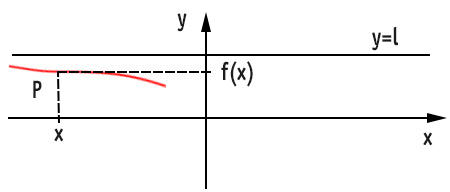
Come si vede dalla figura, data la figura segnata in rosso, quando l’ascissa del punto P si avvicina a -∞, la sua ordinata si avvicina sempre di più alla y della retta asintoto orizzontale.
Asintoto orizzontale esempio
Determiniamo le equazioni dei possibili asintoti orizzontali delle seguenti funzioni, rappresentandone il grafico probabile agli estremi del dominio.
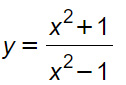
Svolgimento
Bisogna calcolare i limiti di y agli estremi:
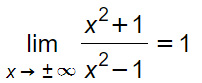
Calcolando l’asintoto orizzontale della funzione fratta si nota che sia a destra che a sinistra la funzione tende a +1. Possiamo scrivere che:
y=1
è un asintoto orizzontale. Dal punto di vista grafico possiamo dedurre che:
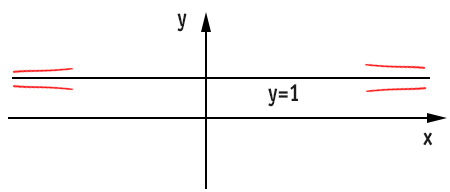
Questo significa che la funzione a più infinito e meno infinito tende a +1, ma in assenza di ulteriori informazioni non sappiamo se vi tende dall’alto o dal basso. Per avere quest’ulteriore informazione dovremmo conoscere anche gli eventuali asintoti verticali e il dominio.