Asintoto obliquo: definizione, formule ed esercizi svolti

L’asintoto obliquo è una retta che indica l’andamento di una funzione ai suoi estremi. Per il calcolo degli asintoti obliqui è necessario che siano verificate tre condizioni, semplici ma indispensabili.

In questa lezione vedremo tutto quello che c’è da sapere sul calcolo dell’asintoto obliquo, illustrandone non solo la forma, ma anche i grafici che si ottengono attraverso lo studio dei limiti che ne consegue. Troverai nella seconda parte della pagina alcuni esempi ed esercizi svolti con i casi più frequenti che si incontrano nello studio di funzione.

Calcolo asintoto obliquo

Immaginiamo una funzione f(x) definita in un intervallo illimitato. Questo significa che dallo studio del dominio della funzione non vengono esclusi più infinito e meno infinito. Allora l’equazione della retta y=mx+q rappresenta un asintoto obliquo se sono verificate tutte le seguenti condizioni.

Condizione 1

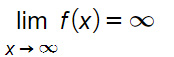
Il limite della funzione, per x che tende a infinito, deve essere pari a infinito.

Questa condizione esclude per definizione la presenza di un asintoto orizzontale, visto lo stesso limite avrebbe dovuto portare ad un valore finito. Nel calcolo degli asintoti obliqui invece è fondamentale che i limiti, per x che tende a infinito, siano infinito.

Se questa prima condizione non risulta verificata, è inutile verificare le altre due. Abbiamo infatti già la certezza che non esiste asintoto obliquo.

Condizione 2

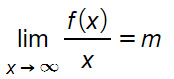
Il limite, per x che tende a infinito, della funzione intera fratto x, è pari ad un numero finito che indichiamo con la lettera m.

Se la condizione 2 risulta essere soddisfatta, allora possiamo verificare la terza e ultima condizione. Nel caso in cui invece il limite non dovesse esistere o se il limite è infinito, allora non esiste asintoto obliquo. Quella che abbiamo indicato con la lettera “m” sarà il coefficiente angolare della retta asintotica obliqua.

Condizione 3

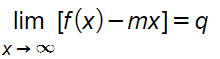
Il limite per x che tende a infinito della funzione a cui si sottrae “m·x” è un numero finito e viene indicato con la lettera q.

Se il limite non dovesse esistere o dovesse essere infinito, allora possiamo scrivere che non esiste asintoto obliquo. In caso contrario abbiamo verificato le tre condizioni e ricavato i coefficienti m e q della retta. Possiamo quindi scrivere che:

Asintoti obliqui destro e sinistro

Nella prima condizione abbiamo verificato che il limite della funzione per x che tende a infinito fosse pari a infinito. Se la condizione vale sia per x→+∞ che per x→-∞ , allora bisogna calcolare i limiti delle condizioni 2 e 3 anche per x→-∞, perché potrebbero esserci due asintoti obliqui differenti.

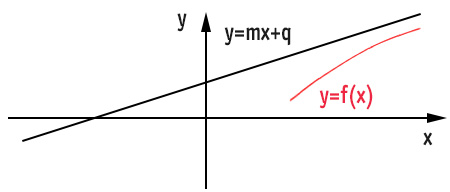
Grafico di un asintoto obliquo

La funzione f(x), man mano che la sua ascissa procede verso infinito, si avvicina sempre di più alla retta asintoto obliquo.

OSSERVAZIONE: In questo grafico abbiamo ipotizzato che la funzione, prima di tendere a infinito, venisse dal basso. In realtà con il solo calcolo dell’asintoto obliquo non possiamo dirlo. Per poter sapere con certezza l’andamento della curva è necessario studiarne il dominio, la studio del segno e le intersezioni con gli assi.

Esempio

Trovare gli asintoti obliqui, se esistono, della seguente funzione.

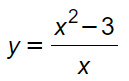
Svolgimento

Per verificare il calcolo dell’asintoto obliquo vanno verificate le tre condizioni. Partiamo dalla prima: limite per x che tende a infinito della funzione. Se il risultato è infinito, allora possiamo proseguire.

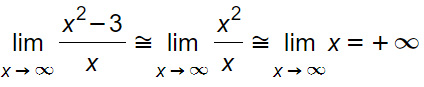
Resta quindi verificata la prima condizione. Analizziamo le altre due.

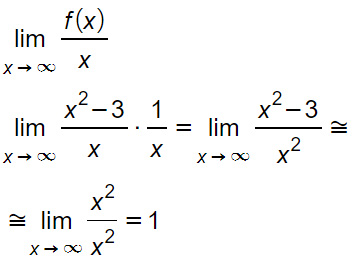
m=1

Anche la seconda condizione è verificata, procediamo quindi con l’ultima.

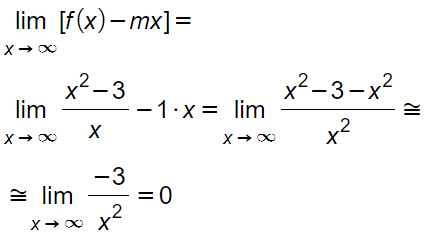
q=0

Andando a riepilogare i dati ottenuti nell’esercizio, m=1 e q=0, per cui la retta y=mx+q diventa:

y=x → asintoto obliquo

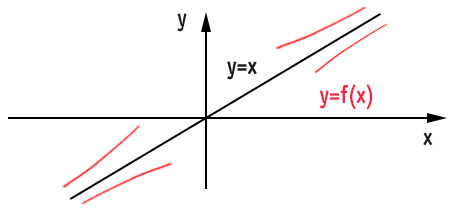
Osservazioni

Come puoi vedere, nel grafico dell’esercizio precedente è stata disegnata la curva anche in corrispondenza di meno infinito. Prova a calcolare i limiti nel caso in cui x tende a meno infinito. Vedrai che uscirà la stessa identica retta.

Puoi anche notare che il grafico più probabile, con le informazioni ricevute con il calcolo dell’asintoto obliquo, tende alla retta y=x sia dall’alto che dal basso. Per scoprirne il comportamento è necessario calcolare il dominio della funzione, studio del segno, …

Conclusioni

In questa lezione abbiamo visto come non esista un’unica formula per l’asintoto obliquo, ma ci siano piuttosto 3 condizioni da soddisfare. Per risolvere gli esercizi senza commettere errori, procedi dalla prima condizioni e verificale una alla volta. Ne basta una che non sia verificata per cui il calcolo degli asintoti obliqui può considerarsi concluso.