Come si calcola l’area del trapezio rettangolo? Quali formule si usano generalmente nei problemi di geometria?
In questa lezione vedremo come calcolare l’area di un trapezio rettangolo analizzandone non solo la formula ma vedendo anche alcuni esercizi svolti e commentati.
Area trapezio rettangolo formula
Esiste un’unica formula ed è abbastanza facile da ricordare: somma delle basi per altezza diviso due.
E’ quindi la stessa che abbiamo visto nella lezione sulle formule del trapezio, con la particolarità che l’altezza in questo caso coincide con uno dei due lati obliqui.
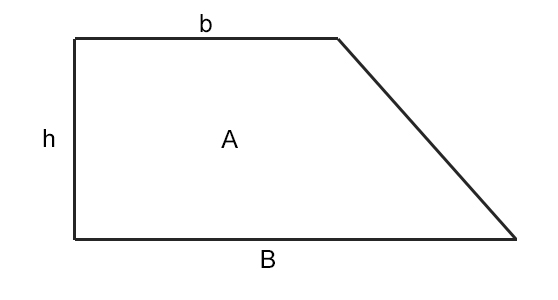
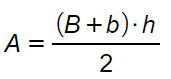
Come si calcola l’area del trapezio rettangolo?
Dato quindi un trapezio rettangolo, siano B la base maggiore, b la base minore, h l’altezza e A la misura dell’area.
E’ sufficiente fare base maggiore più base minore, per altezza diviso due.
Potrebbe interessarti anche: come calcolare l’area di un trapezio isoscele
Come calcolarla se manca l’altezza…
… ed è noto il lato obliquo
Nel caso in cui la traccia ci dia la misura del lato obliquo, allora dobbiamo calcolare la misura dell’altezza, attraverso pochi semplici calcoli.
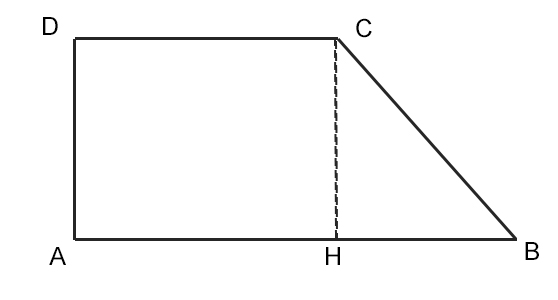
Innanzitutto si considera il triangolo rettangolo CHB di cui è nota l’ipotenusa BC. Possiamo calcolare anche il cateto HB facendo la sottrazione tra le due basi del trapezio. Cioè:
AB-DC=HB
A questo punto, applicando la formula inversa del teorema di Pitagora, si calcola il cateto del triangolo CH che è anche l’altezza del trapezio rettangolo. Infine si determina l’area con la formula vista sopra.
… ed è nota la diagonale minore
Nel caso in cui l’altezza sia da calcolare e la traccia del problema fornisce la misura della diagonale minore AC, allora consideriamo il triangolo AHC in figura sotto.
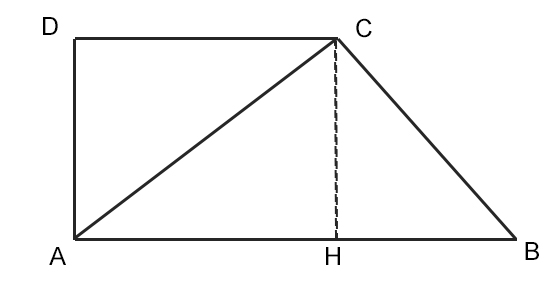
Si tratta di un triangolo rettangolo di cui è nota l’ipotenusa AC (proprio la diagonale) e il cateto AH che è uguale alla base minore DC.
Si può quindi applicare come prima la formula inversa di Pitagora per ottenere il cateto CH. L’area del trapezio rettangolo la si calcola infine con la formula vista sopra.
… ed è nota la misura della diagonale maggiore
Nel caso in cui sia nota la misura delle basi e della diagonale maggiore, si va a considerare il triangolo rettangolo ABD come nella figura in basso.
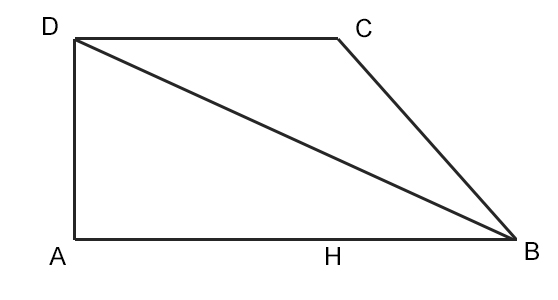
Conosciamo la misura del cateto AB e dell’ipotenusa DB. Possiamo applicare ancora una volta la formula inversa di Pitagora per ottenere l’altezza DA. Da qui poi sarà semplice concludere con il calcolo dell’area del trapezio.
Esercizi svolti sull’area del trapezio rettangolo
Esercizio 1
Calcolare l’area di un triangolo rettangolo che ha le basi che misurano rispettivamente 59 cm e 35 cm e l’altezza di 18 cm.
Svolgimento
Il calcolo è estremamente semplice: basta applicare la formula vista sopra visto che abbiamo tutti i dati a disposizione.
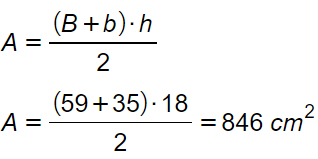
Esercizio 2
La differenza delle basi di un trapezio rettangolo è 40 cm. Sapendo che la base minore è 2/3 della base maggiore e che l’altezza misura 30 cm, calcolare la misura dell’area del trapezio rettangolo.
Svolgimento
Per fare un po’ di chiarezza, facciamo subito il disegno della figura e analizziamo i dati a disposizione.
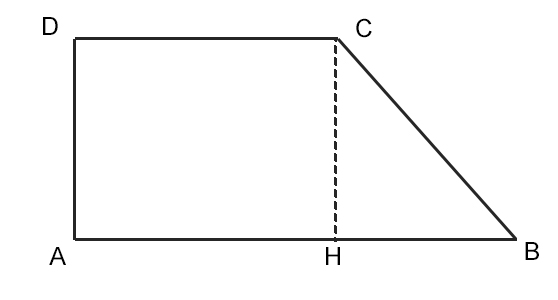
Sappiamo che il segmento HB misura 40 cm perché è la differenza delle basi. Abbiamo anche la misura del segmento CH, ovvero l’altezza. Sappiamo infine che DC=2/3 di AB.
Per gli studenti delle scuole superiori consigliamo di porre il segmento AB=x e di risolvere una semplice equazione di primo grado. Per gli studenti delle scuole medie invece disegniamo i segmenti che ci interessano come di seguito:
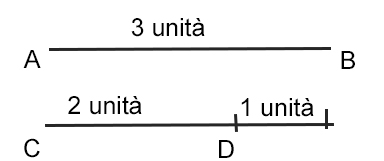
La differenza tra le basi AB-CD=40 cm = 1 unità.
Per cui:
- AB = 3 unità = 3·40 cm = 120 cm
- CD= 2 unità = 2·40 cm = 80 cm
Possiamo infine calcolare l’area:
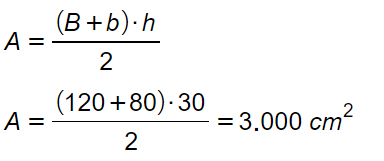
Conclusioni
In questa breve lezione abbiamo alcuni dei possibili casi che si possono incontrare nei problemi di geometria sul calcolo dell’area del trapezio rettangolo.
Se gli appunti ti sono stati utili, se hai delle domande o dei dubbi, non esitare a lasciare un commento. Il nostro staff è a tua disposizione.