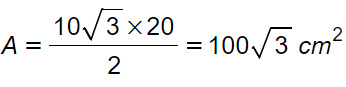Come si calcola l’area del rombo? Quali formule possono essere usate avendo a disposizione diagonali, lati o perimetro? E’ possibile avere qualche esercizio svolto sul calcolo dell’area del rombo? – Claudio
Risposta
Per capire come si trova l’area del rombo è importante riconoscere quali sono i dati a disposizione. A seconda che si hanno le diagonali, la misura del lato o il perimetro, è possibile utilizzare delle formule differenti.
Area del rombo formula
In questo piccolo formulario, vedremo 2 possibili casi che si possono incontrare nello svolgimento degli esercizi. In basso vedremo la dimostrazione di ogni formula, cioè come si arriva ad ottenerla in pochi semplici passaggi.
Area del rombo con le diagonali
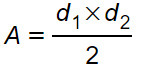
Area del rombo noto il lato
![]()
Dove d1 e d2 sono le diagonali, A è l’area, L è la misura del lato, mentre h è l’altezza relativa a quel lato, come mostrato nella figura seguente.
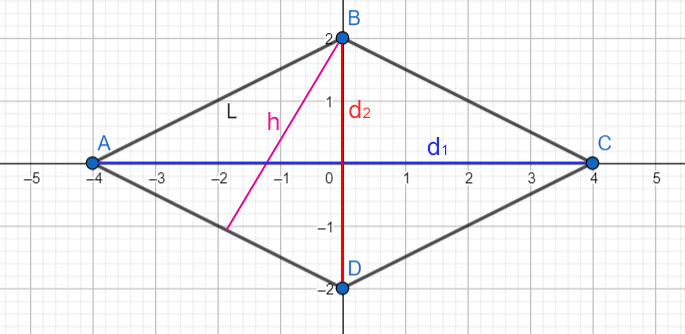
Come si trova l’area del rombo conoscendo le diagonali
E’ il caso più frequente che si incontra nei problemi di geometria. Si conosce la misura della diagonale minore e di quella maggiore.
Nella figura in alto possiamo vedere che le due diagonali si intersecano perpendicolarmente formando quattro triangoli rettangoli. Le due semi diagonali sono i cateti, mentre il lato è l’ipotenusa.
Per cui possiamo scrivere:
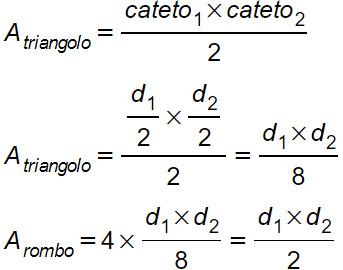
Come si calcola l’area del rombo conoscendo il lato
La seconda formula si basa invece su un’osservazione piuttosto semplice. Prova a ruotare la figura del rombo in alto. Ti accorgerai che non è altro che un parallelogramma ruotato di 90°, per cui la misura dell’area è base per altezza.
Poiché la base è il lato, allora l’are di un rombo si può calcolare anche come lato per la misura dell’altezza relativa a quel lato.
Esercizi svolti
La parte teorica si è già conclusa. Per il formulario completo su questa figura geometrica, ti consigliamo di consultare la nostra lezione sulle formule del rombo.
In questa seconda parte della lezione vedremo in maniera pratica come si trova l’area del rombo vedendo dei problemi risolti e commentati. Iniziamo subito.
Esercizio 1
Calcolare l’area di un rombo che ha le diagonali che misurano 10 cm e 5 cm.
Svolgimento
Il primo esercizio è estremamente semplice. Ci sono già i tutti i dati a disposizione per usare la prima formula vista, per cui possiamo scrivere:
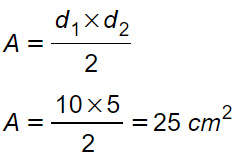
Esercizio 2
Calcolare l’area di un rombo che ha il lato che misura 15 cm e una delle due diagonali che misura 20 cm.
Svolgimento
Ecco un esercizio più interessante. Non abbiamo la formula diretta per l’area noti lato e diagonale. O usiamo la formula con lato e altezza o quella con le due diagonali.
Notiamo che le diagonali dividono la figura in 4 triangoli rettangoli di cui conosciamo ipotenusa e un cateto (basta dividere la diagonale per due).
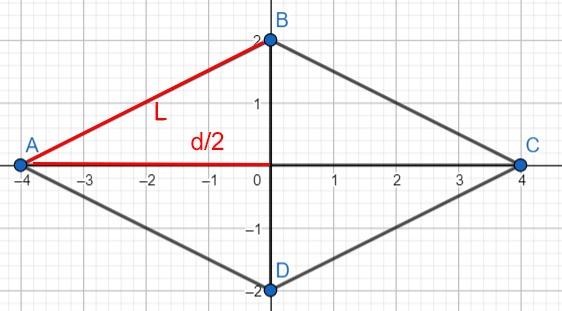
Per cui:
- ipotenusa = 15 cm
- cateto = 20 cm : 2 = 10 cm
Possiamo applicare la formula inversa del teorema di Pitagora, così da calcolare l’altro cateto. Moltiplicando la misura per 2 ottengo la seconda diagonale.
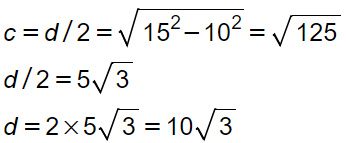
Per il calcolo dell’area del rombo, basta ora la formula con il semi-prodotto delle diagonali.