Che cos’è un angolo convesso? In questa lezione vediamo una definizione sugli angoli convessi ed alcuni esempi per rendere più chiaro l’argomento.
Definizione angolo convesso
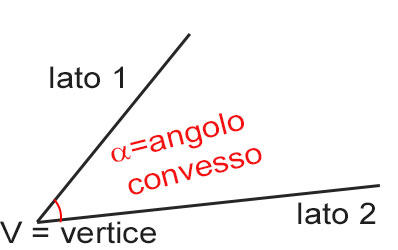
Si parla di angolo convesso quando non contiene il prolungamento dei lati.
E’ la definizione che puoi trovare in tutti i libri di geometria, ma diversi studenti ci hanno chiesto di spiegarla meglio perché non è sufficientemente chiara.
Quando si ha un angolo convesso? Cosa sono i prolungamenti dei lati? Che differenza c’è tra un angolo convesso e concavo? Cerchiamo di rispondere con calma a tutti questi dubbi.
Ti ricordi qual è la definizione di angolo? E’ quella parte di piano che si forma dall’intersezione di due semirette. Il punto di intersezione si chiama vertice, mentre le semirette che formano l’angolo si chiamano lati.
A questo punto prova ad immaginare di prolungare i lati oltre il vertice, così come nella figura che segue.
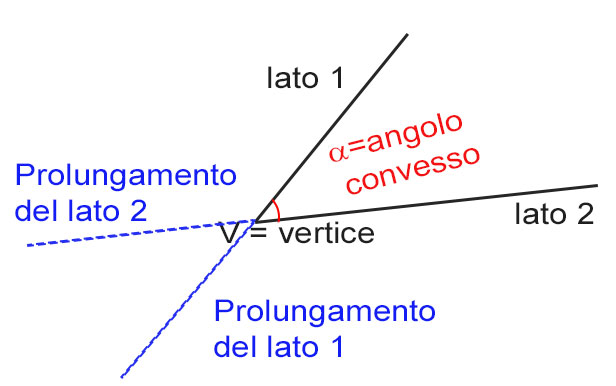
Come puoi notare l’angolo convesso non contiene il prolungamento dei lati, ma si trova all’interno dello spazio compreso tra il lato 1 e il lato 2.
La differenza tra angoli convessi e concavi è proprio questa. Quello rosso disegnato nella figura è l’angolo convesso, dall’altra parte si genera invece l’angolo concavo.
Misura di un angolo convesso
Qual è l’ampiezza degli angoli convessi? Come puoi vedere dalla figura, il concavo sarà sempre minore del convesso. In particolare possiamo dire che per un angolo concavo vale:
0<α<180°
Si può esprimere il valore dell’angolo in radianti e scrivere che:
0<α<2π
DOMANDA 1 : un angolo piatto è concavo o convesso? Nessuno dei due. Infatti l’angolo con ampiezza di 180° è l’unico che non può essere considerato né concavo né convesso.
L’angolo nullo invece rientra nella categoria degli angoli convessi.
L’angolo retto è da considerare come un angolo convesso.
DOMANDA 2: un angolo concavo è acuto o ottuso? Può essere entrambi. Sicuramente un angolo acuto è concavo. Non necessariamente un angolo ottuso è concavo.
Conclusioni
La lezione di oggi è valida sia per gli studenti delle scuole primarie che per quelli delle superiori. Per qualsiasi dubbio o richiesta, non esitare a scrivere nei commenti. Il nostro staff è a tua disposizione e ci aiuterai così a migliorare la qualità delle lezioni.