Quali sono gli angoli supplementari? Di quali proprietà godono? In questa lezione vedremo un approfondimento semplice ma completo su tutto ciò che riguarda gli angoli supplementari, dalla definizione fino a qualche semplice esempio.
Molto spesso gli studenti si confondono e sbagliano la differenza tra angoli supplementari e complementari. Grazie a questa breve lezione vedremo alcuni trucchetti per ricordare l’argomento in maniera più facile.
Angoli supplementari: definizione
Due angoli sono supplementari quando la loro somma è pari ad un angolo piatto.
Poiché quest’ultimo è pari a 180°, possiamo anche dire che due angoli si dicono supplementari se la loro somma è uguale a 180°.
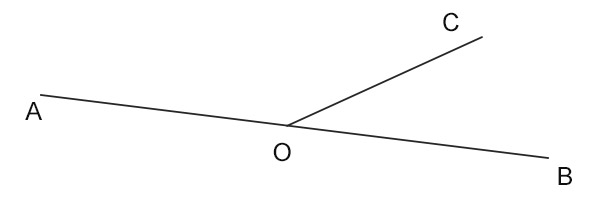
Nella figura abbiamo due AOC e COB che sono due angoli consecutivi la cui somma è pari all’angolo piatto AOB.
AOC+BOC=AOB=180°
Da notare che si tratta anche di angoli adiacenti visto che hanno il vertice O e il lato OC in comune e i lati AO e OB allineati lungo una retta.
Angoli supplementari – esercizi svolti
Esercizio 1
La differenza di due angoli supplementari misura 140°. Calcolare l’ampiezza dei due angoli.
Svolgimento
La data ci fornisce due dati, la somma e la differenza. Detti AOB e BOC i due angoli, eseguiamo per prima cosa il disegno.
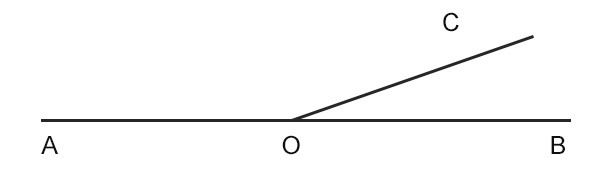
I dati sono:
AOC+COB=180°
Immaginiamo che la misura dei due angoli da calcolare possa essere disegnata come un segmento. Allora possiamo disegnare:
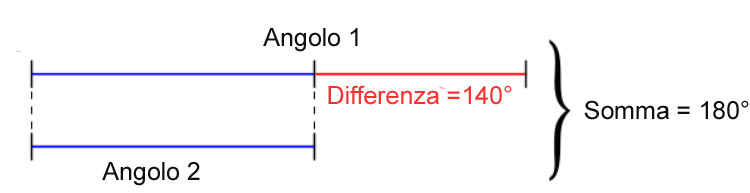
Dall’immagine puoi vedere che se dalla somma sottraiamo la differenza (cioè il segmento in rosso) ci restano i due segmenti blu, che sono tra loro uguali.
Quindi vuol dire che:
180°-140°=2·COB
COB=40°:2 = 20°
Per calcolare l’ultima incognita (cioè AOB), sappiamo che gli angoli sono supplementari, per cui se uno misura 20°, l’altro necessariamente sarà 160°.
AOB=160°
Esercizio 2
Calcola la misura dell’angolo supplementare dell’angolo 47° 28′.
Svolgimento
L’esercizio ci chiede di calcolare la misura di un angolo che, sommato a 47°28′ mi dia come risultato 180°.
Ciò si traduce come una semplice sottrazione:
α=180°-47°28′
Ti ricordi come si fanno le sottrazioni tra angoli? Mettiamo in colonna, ricordando che vale il sistema di misura sessagesimale, quindi ad 1° corrispondono 60′.

Quindi eseguendo una semplice differenza abbiamo calcolato l’incognita che è pari a 132° 32′.
Esercizio 3
Calcola la misura di due angoli supplementari, sapendo che uno è il quadruplo dell’altro.
Svolgimento
In base ai dati che ci vengono forniti dalla traccia, possiamo scrivere che:
α+β=180°
α=4β
Anche in questo caso gli studenti delle scuole superiori possono utilizzare le equazioni di primo grado indicando con β=x, da cui si ricava che α=4x, per cui x+4x=180°. Da qui si arriva alla soluzione in un paio di semplici passaggi.
Per gli studenti delle scuole medie, invece, proviamo a ragionare sempre con i segmenti.
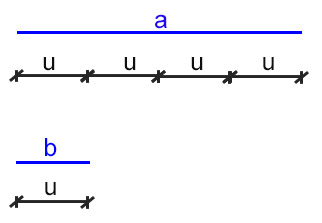
L’angolo α vale 4 unità (cioè 4 segmenti), mentre β vale 1 unità (cioè 1 segmento). Vuol dire che in totale ci sono 5 segmenti e la loro somma vale 180°. Quindi possiamo scrivere:
5u=180°
u=36°
Per cui:
β = 1u = 36°
α = 4u = 4·36° = 144°
Per verificare che il risultato sia giusto, basta sommare le due soluzioni ottenute. Poiché 144°+36° è uguale 180°, allora il risultato è esatto.