Angoli esplementari – definizioni ed esercizi svolti

Quali sono gli angoli esplementari? Di quali proprietà godono? Ecco una lezione completa con definizioni, figure ed esercizi svolti.

Impareremo che cos’è un angolo esplementare e come risolvono gli esercizi in maniera semplice e senza rischio di sbagliare. Partiamo subito dalla definizione.

Angoli esplementari: definizione

Si definiscono angoli esplementari, due angoli la cui somma è pari a 360°.

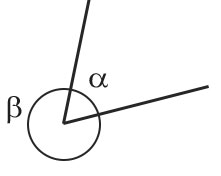
In figura si vedono due angoli consecutivi α e β, che sommati fanno proprio 360°. Una definizione alternativa può essere:

Due angoli sono esplementari quando sommati formato un angolo giro.

Proprietà

• Se ad essere sommati sono soltanto due angoli, affinché la loro somma sia 360°, almeno uno dei due deve essere un angolo ottuso, cioè con ampiezza superiore ai 90°.
• Si definisce invece angolo esplementare α di un angolo β, quell’angolo α la cui ampiezza deve essere tale che sommato a β dia un risultato pari a 360°

Esempio 1

L’angolo esplementare di un angolo giro è l’angolo nullo. 

Questo perché se α=360° e sappiamo che α+β=360° (perché angoli esplementari), allora β=0°.

Esempio 2

L’angolo esplementare di un angolo piatto è un altro angolo piatto

Questo perché se α=180° e sappiamo che α+β=360° (perché angoli esplementari), allora β=180°.

Esercizi svolti sugli angoli esplementari

Problema 1

La differenza di due angoli esplementari è 120°. Determinare la misura dei due angoli.

Svolgimento

Gli studenti delle scuole superiori possono risolvere questo problema con un sistema di primo grado a due incognite. Le equazioni sono: x+y=360° e x-y=120°.

Per gli studenti delle scuole medie invece ragioniamo per segmenti unitari. Cioè immaginiamo di poter rappresentare l’ampiezza degli angoli come dei segmenti.

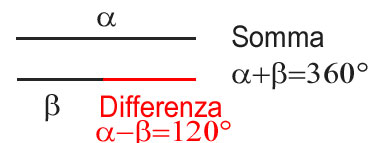
Si nota che se alla somma si sottrae la differenza, escono i due segmenti in nero che hanno stessa lunghezza . Per cui possiamo scrivere che:

360°-120°=2β

Da cui si ricava che:

240°=2β → β=120°

α+β=360° → α+120°=360° → α=240°

Problema 2

Determinare l’ampiezza di due angoli esplementari, sapendo che uno è il triplo dell’altro.

Svolgimento

Gli studenti delle scuole superiori possono risolvere con le equazioni di primo grado. Imponendo β=x, si ottiene che α=3x. Per cui essendo gli angoli esplementari, x+3x=360°, cioè 4x=360°. In questo modo in pochi semplici passaggi si arriva alla soluzione.

Gli studenti delle scuole medie, invece devono ragionare per segmenti unitari.

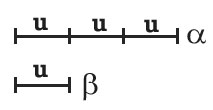
Se alfa lo disegniamo come 3u e beta come 1u, allora in tutto ci sono 4 segmenti, la cui somma è pari a 360°. Per cui possiamo scrivere che:

4u=360° → u=90°

Poiché β=u, allora:

β=90°
α=3β=3·90°=270°.

Conclusioni

Abbiamo visto che la tecnica di risoluzione degli esercizi sugli angoli esplementari è identica a quella usata con gli angoli complementari e supplementari.

Ovviamente l’unica cosa che cambia è la somma, che nel caso di un angolo esplementare è pari a 360°.

Se questa lezione ti è stata d’aiuto o se hai altri esercizi da proporre, lascia un commento in basso. Un tuo feedback positivo ci aiuterà a migliorare la qualità delle lezioni giorno dopo giorno.