Angoli associati – che cosa sono e a cosa servono? Definizioni ed esercizi svolti

Gli angoli associati sono degli angoli che, attraverso delle somme o delle differenze, possono essere ricondotti ad angoli noti appartenenti al primo quadrante. Sono particolarmente utili per evitare di imparare a memoria tutti i valori delle funzioni trigonometriche, così da ricavarli in pochi istanti quando necessario.

Abbiamo già trattato l’argomento in maniera più dettagliata nella lezione riguardante gli archi associati. In questa pagina vedremo un riepilogo delle definizioni e delle formule degli angoli associati da usare. Troverai infine alcuni esercizi svolti per fare pratica con gli argomenti trattati.

Definizione di angoli associati

Dato l’angolo α della circonferenza goniometrica in figura sotto, dal punto B tracciamo le parallele agli assi cartesiani, BC e BE ed i diametri BD e CE.

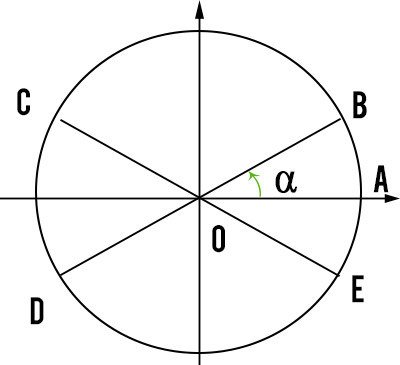
Gli archi AB, AC, AD e AE, aventi ampiezza rispettivamente pari a α, 180°-α, 180°+α, 360°-α si dicono angoli associati (o archi associati) e hanno i valori di seno, coseno, tangente e cotangente uguali in valore assoluto. Questo significa che cambiano solo i segni, ma i numeri restano gli stessi.

Se invece vogliamo esprimere tutto in radianti, allora le formule degli angoli associati vanno riferite a: α, π-α, π+α, 2π-α.

Angoli associati tabella

Angoli associati supplementari (α, 180-α)

sin(180°-α)=sinα
cos(180°-α)=-cosα
tg(180°-α)=-tgα
cotg(180°-α)=-cotgα

Angoli associati che differiscono di 180° (α. 180°+α)

sin(180°+α)=-senα
cos(180°+α)=-cosα
tg(180°+α)=tgα
cotg(180°+α)=cotgα

Angoli associati esplementari (α,360-α) ed opposti (α, -α)

sin(360°-α)=sin(-α)=-senα
cos(360°-α)=cos(-α)=cosα
tg(360°-α)=tg(-α)=-tgα
cotg(360°-α)=cotg(-α)=-cotgα

Angoli associati complementari (α,90-α)

A differenza dei casi precedenti, con gli angoli complementari cambia anche il valore assoluto del risultato. Cioè la funzione goniometrica non si conserva ma si invertono. Cioè il seno diventerà coseno e viceversa.

sin(90°-α)=cosα
cos(90°-α)=senα
tg(90°-α)=cotgα
cotg(90°-α)=tgα

Angoli associati complementari (α,90+α)

sin(90°+α)=cosα
cos(90°+α)=-senα
tg(90°+α)=-cotgα
cotg(90°+α)=-tgα

Angoli associati aventi per somma 270° (α,270-α)

sin(270°-α)=-cosα
cos(270°-α)=-senα
tg(270°-α)=cotgα
cotg(270°-α)=tgα

Angoli associati aventi per somma 270° (α,270-α)

sin(270°+α)=-cosα
cos(270°+α)=senα
tg(270°+α)=-cotgα
cotg(270°+α)=-tgα

La precedente tabella con le formule può essere riscritta utilizzando la misura in radianti degli angoli. Non cambia nulla, basta sostituire π al posto di 180° e 2π al posto di 360°.

Ricordiamo infine che gli angoli α e α+2kπ hanno le stesse funzioni goniometriche. Ne consegue che l’angolo -α risulta essere associato ad α, poiché ha le stesse funzioni goniometriche dell’angolo 360°-α.

Angoli associati esercizi

Esercizio 1

Determinare gli angoli associati supplementari e giro a quelli dati: 32°, 101°, 189°, 315°.

Svolgimento

In questo caso la misura degli angoli è espressa in gradi. Se α è l’angolo assegnato dalla traccia del problema, gli angoli associati sono: 180°-α, 180°+α, 360°-α. Per cui cominciamo dal primo:

• α=32°
  180°-α=180°-32°=148°
  180°+α=180°+32°=212°
  360°-α=360°-32°=328°

Osserviamo che se alfa è un angolo appartenente al primo quadrante, i suoi angoli associati hanno estremi rispettivamente nel secondo, terzo e quarto quadrante.

• α=101°
  180°-α=180°-101°=79°
  180°+α=180°+101°=281°
  360°-α=360°-101°=259°

Osserviamo che se alfa è un angolo avente un estremo nel secondo quadrante, i suoi angoli associati hanno estremo, rispettivamente, nel primo, nel terzo e nel quarto quadrante.

• 189°
  180°-α=180°-101°=79°
  180°+α=180°+101°=281°
  360°-α=360°-101°=259°

In questo caso si nota che se alfa è un angolo situato nel terzo quadrante, i suoi angoli associati si trovano invece nel quarto, nel primo e nel secondo quadrante.

• 315°
  180°-α=180°-315°=-135°
  180°+α=180°+315°=495°
  360°-α=360°-315°=45°

In quest’ultimo caso notiamo che se alfa appartiene al quarto quadrante, allora i suoi angoli associati si trovano nel terzo, nel secondo e nel primo quadrante.

Esercizio 2

Sfruttando le relazioni tra le funzioni goniometriche degli angoli associati, semplificare le seguenti espressioni:

1. sen(π-α)-cos(π+α)-cosα-sen(-α)·cotgα
2. cotg(180°+α) + tg(360°-α) + [sen(180°-α)-cosα]/cos(-α)

Svolgimento

sen(π-α)-cos(π+α)-cosα-sen(-α)·cotgα=

= senα+cosα-cosα+senα·cosα/senα=

= senα+cosα.

cotg(180°+α) + tg(360°-α)+ [sen(180°-α)-cosα] / cos(-α)=

= cosα/senα – senα/cosα + (senα-cosα)/cosα =

Essendoci un denominatore dobbiamo calcolare il minimo comune multiplo.

= (cos²α-sen²α+sen²α-cosαsenα) / senαcosα =

= (cos²α-cosα·senα)/senαcosα =

A questo punto basta eseguire una messa in evidenza totale al numeratore.

= cosα (cosα-senα)/senαcosα =

= (cosα-senα)/senα.

Esercizio 3

Sfruttando le relazioni viste tra gli angoli associati, semplificare le seguenti espressioni algebriche.

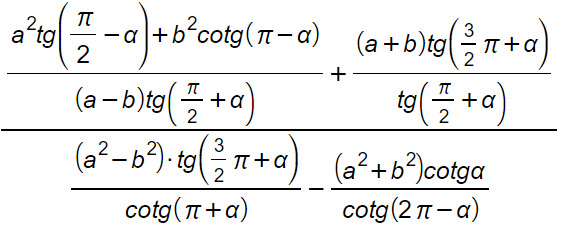
Svolgimento

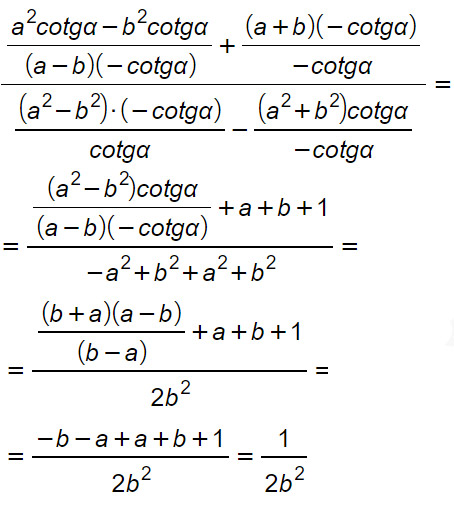
Essendoci dei denominatori, è necessario imporre le condizioni di esistenza come si faceva in genere con le equazioni razionali fratte. Per cui l’espressione ha senso solo se:

a≠b, b≠0, a≠kπ/2

Conclusioni

Gli angoli associati, come visto in questa lezione si risolvono semplicemente facendo riferimento a delle formule. Con il passare del tempo, facendo un po’ di pratica, inizierai a ricordarle e tutto sarà molto più semplice.

Se questa lezione ti è stata utile, o se hai ancora dei dubbi o delle domande da fare, lascia un commento in basso. Ci aiuterai a migliorare la qualità degli appunti e degli esercizi messi a disposizione.