Nicholas, studente delle scuole medie, ci chiede un approfondimento di geometria: come trovare l’altezza di un triangolo equilatero? Esiste un formulario da seguire o delle regole da tenere in considerazione quando risolvo i problemi?
RISPOSTA
Prima di andare alle formule diamo una piccola definizione.
Altezza triangolo equilatero: è il segmento che unisce uno dei vertici del triangolo equilatero con il lato opposto. Essendoci tre vertici, possiamo quindi disegnare 3 altezze, così come nella figura che segue.
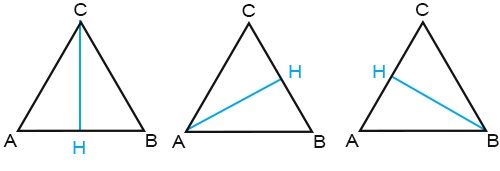
CH = altezza relativa al lato AB
AH = altezza relativa al lato CB
BH = altezza relativa al lato AC
Poiché un triangolo equilatero ha tutti i lati congruenti, le tre altezze sono uguali tra loro e ciascuna è anche asse, mediana e bisettrice.
Formula altezza triangolo equilatero
La misura dell’altezza di un triangolo equilatero può essere determinata usando le formule inverse per il calcolo del perimetro e dell’area in maniera più elementare. Si può ricavare però anche con il raggio della circonferenza circoscritta o inscritta.
Approfondimenti: area triangolo equilatero
NOTO IL LATO: di seguito trovi una formula che puoi applicare direttamene ma che sconsigliamo perché potrebbe essere valutato come errato dai docenti perché deriva da argomenti non ancora affrontati.
Il metodo corretto per studenti delle scuole elementari e medie consiste nell’applicazione del teorema di Pitagora. E’ sufficiente infatti dividere in 2 la base e calcolare l’altezza del triangolo equilatero applicando la formula inversa di Pitagora. Vai all’esercizio n.1 per un esempio pratico.

Questa prima formula si ottiene semplicemente facendo la formula inversa di base per altezza diviso 2.

La seconda formula la otteniamo invece a partire dal raggio della circonferenza circoscritta, ricordando che il lato del triangolo è pari al raggio moltiplicato radice di 3.

Dove R è il raggio della circonferenza inscritta all’interno del triangolo equilatero.

Se sei alle scuole medie quest’ultima formula è meglio evitare di utilizzarla, perché si ottiene dai teoremi sui triangoli rettangoli in trigonometria.
Altezza ed angoli
L’altezza di un triangolo equilatero divide inoltre la figura in due triangoli rettangoli uguali. Ricordando che la somma degli angoli interni è 180°, allora ogni angolo misura 60°.
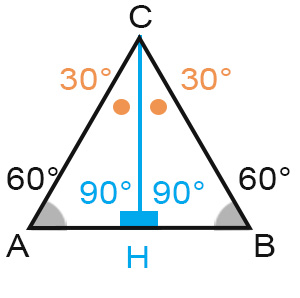
Quelli che si formano sono due triangoli di 30 60 90 (per ulteriori informazioni vai alla lezione sui tipi di triangoli).
Problemi risolti ed esercizi svolti
Esercizio 1
Calcola la misura dell’altezza di un triangolo equilatero che ha il lato di 14 cm.
Svolgimento
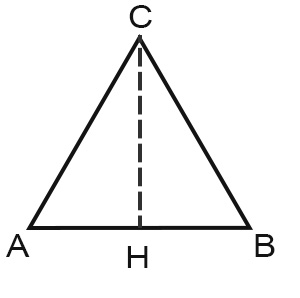
Sappiamo dalla traccia che AC=AB=BC=14 cm. Possiamo quindi dividere in 2 la base e scrivere che AH=7 cm.
Considerando il triangolo AHC, applichiamo la formula inversa di Pitagora: abbiamo nota l’ipotenusa AC e il cateto AH, dobbiamo calcolare il cateto maggiore CH.
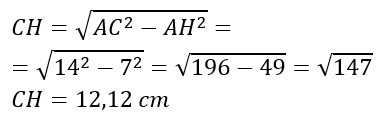
Esercizio 2
Sapendo che l’altezza del triangolo equilatero vale 4,33 cm, calcolare la misura del lato.
Svolgimento
Problema inverso rispetto al precedente. Abbiamo l’altezza, ma serve il lato. Come procedere? Ricorriamo all’ultima formula, sfruttandone la sua inversa.
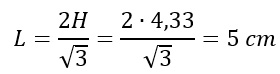
Conclusioni
Speriamo in questa lezione di aver chiarito tutti i dubbi di Nicholas sull’altezza del triangolo equilatero, ma invitiamo tutti gli studenti a prendere parte alla discussione lasciando un commento in basso. Hai un esercizio da risolvere o hai apprezzato la qualità della lezione? Lasciaci un feedback, ci aiuterai a migliorare la qualità degli appunti che scriviamo per te ogni giorno. Buono studio!
bella lezione