Giulia ci scrive: “Qual è la derivata del logaritmo? Mi potreste spiegare la differenza tra derivata logaritmo naturale e uno con una base diversa a e? Come si dimostra il risultato della derivata di log(x)?
RISPOSTA
La derivata di un logaritmo fa parte di quelle che vengono definite derivate fondamentali e si può sintetizzare nella formula:
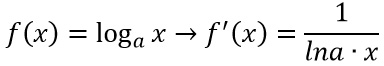
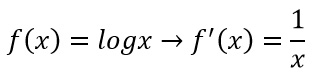
Le due formule che hai visto riguardano la derivata del logaritmo con generica base a e la derivata del logaritmo naturale, cioè con base il numero di Nepero e. Come si arriva al calcolo di questa operazione tanto frequente negli esercizi di analisi?
Derivata logaritmo dimostrazione
La dimostrazione si esegue sviluppando la definizione di derivata, ovvero calcolando il limite del rapporto incrementale. Ti ricordi qual è la formula? Rivediamola insieme:
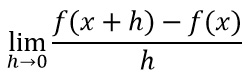
Al posto di f(x) mettiamo il log(x) e al posto di f(x+h) metteremo log(x+h).
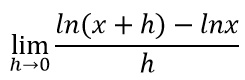
Arrivati a questo punto andiamo a rispolverare le proprietà dei logaritmi. Tra queste scegliamo ed applichiamo la regola della differenza di logaritmi: cioè la sottrazione si trasforma in un rapporto degli argomenti.
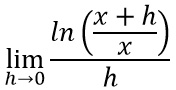
A questo punto scomponiamo il rapporto (x+h)/x dividendolo in due addendi:
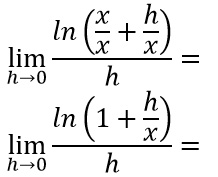
Il limite appena individuato ci ricorda moltissimo i limiti notevoli sui logaritmi:
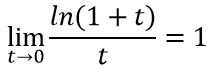
Per poter utilizzare il limite notevole è necessario porre h/x=t. Quindi andiamo a sostituire tenendo presente che nel denominatore h=tx.
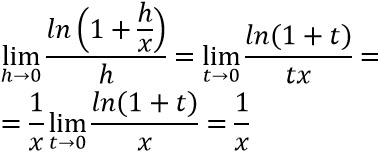
Abbiamo così dimostrato il risultato di partenza. Cerchiamo a questo punto di complicare leggermente il calcolo: cosa succede quando l’argomento del logaritmo è una funzione? Passiamo quindi al calcolo delle derivate di funzioni composte.
Derivata logaritmo fx
Cerchiamo quindi di capire come si può calcolare la derivata del logaritmo di una funzione. La formula da usare è la seguente:
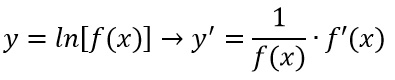
Come puoi vedere si risolve esattamente come prima, ovvero svolgendo la derivata si mette 1 fratto l’argomento del logaritmo, in tal caso la funzione f(x). A questo si moltiplica poi la derivata prima della funzione, quindi f'(x). Proviamo a vedere insieme qualche esempio.
Derivata logaritmo esercizi svolti
ESERCIZIO 1
Calcolare la derivata della seguente funzione:
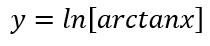
Applichiamo la regola di derivazione per le funzioni composte che abbiamo visto. Quindi il risultato della derivata sarà 1 fratto la funzione – ovvero la funzione arcotangente – moltiplicato per la sua derivata, ovvero la derivata dell’arcotangente.
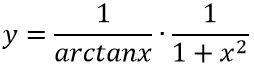
ESERCIZIO 2
Proviamo a risolvere la derivata del logaritmo al quadrato, un problema che si presenta spesso e che alcuni nostri studenti ci hanno chiesto di approfondire.
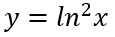
In questo caso non si applica per primo la regola di derivazione del logaritmo, ma applichiamo subito la derivata del quadrato (visto che si tratta di un logaritmo al quadrato). Diverso sarebbe stato il caso, lo vedremo nel prossimo esercizio, se al quadrato fosse stata la x. Per capire cosa derivare per prima, immagina di essere per un secondo la x, quali sono le operazioni che vengono applicate per prima?
- si applica il logaritmo
- si eleva tutto al quadrato
Si parte proprio dall’ultima e si va a salire. Quindi per prima cosa facciamo la derivata del quadrato e poi moltiplichiamo per 1/x che è la derivata del logaritmo:
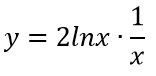
ESERCIZIO 3
A questo punto proviamo a svolgere la derivata di ln x al quadrato.
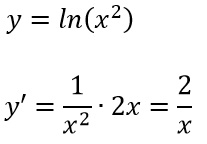
Come puoi vedere in base a come viene posizionato il quadrato – se sul logaritmo o sulla x – cambia il risultato finale dell’operazione.
Se questa lezione ti è stata utile o se hai ancora dei dubbi, delle curiosità lasciaci un feedback nei commenti. Ogni tuo commento positivo ci aiuterà ad offrirti ogni giorno nuove lezioni e ad arricchire queste ultime con le tue domande.