Mario ci scrive: “Qual è la derivata dell’arcoseno di x? Come si dimostra e soprattutto quanto vale la derivata di arcsin f(x), cioè con una funzione all’interno dell’argomento?”
RISPOSTA
La derivata dell’arcoseno di x fa parte delle derivate fondamentali che si trova sotto forma di tabella su qualsiasi libro di analisi o di matematica. Rispondiamo alla domanda di Mario e dei tanti studenti che ci hanno scritto, analizzando subito la formula risolutiva:
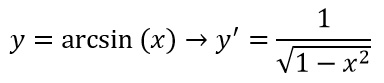
E’ una delle derivate che ti consigliamo di imparare o comunque su cui vale la pena esercitarti. E’ vero che la funzione arcoseno non è molto amata dagli studenti, ma la sua derivata è davvero immediata e proprio per questo è importante fare qualche esercizio, così da imparare automaticamente la formula a memoria: ti capiterà spesso di usarla nei compiti o negli studi di funzione.
Derivata arcoseno: dimostrazione
Nelle lezioni precedenti abbiamo visto come in alcuni casi si possa usare la definizione di derivata per dimostrare le derivate immediate di alcune funzioni (vedi la derivata di x). In altri casi, come per la derivata dell’arcotangente, piuttosto che il metodo del rapporto incrementale conviene utilizzare le regole di derivazione che riguardano le funzioni inverse.
L’arcoseno infatti è l’inversa della funzione seno, per cui se definiamo y=arcosenx, allora la sua inversa sarà f^-1=sen(y) derivata sarà:
Ricorda che la derivata della funzione inversa è uguale ad 1 fratto la derivata della funzione. Per cui possiamo scrivere la seguente uguaglianza:
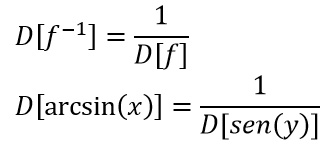
Possiamo quindi risolvere la derivata del seno di x, per ottenere:
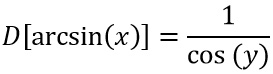
A questo punto, utilizzando le relazioni fondamentali della goniometria, trasformiamo la funzione coseno in seno.
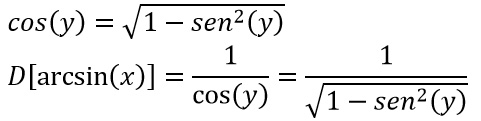
Poiché y=arcoseno di x, allora andiamo a sostituire:
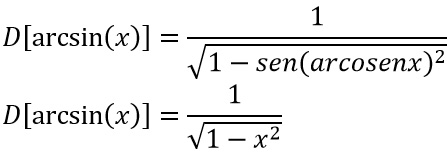
Abbiamo così dimostrato la nostra tesi e il risutato che ti aspettavamo.
Derivata arcoseno f(x)
Concludiamo facendo un breve riferimento alle derivata delle funzioni composte. Cosa succede infatti quando dobbiamo risolvere la derivata dell’arcoseno che ha al suo interno un’ulteriore funzione?
Seguiamo semplicemente la formula che abbiamo visto ma con una piccola modifica. Al denominatore invece di esserci la x ci sarà la f(x) argomento dell’arcoseno e il tutto va poi moltiplicato per la derivata di f(x). Cioè tradotto in formula:
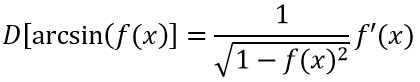
ESERCIZIO SVOLTO
Per chiarire quest’ultimo caso, che sarà anche il più frequente negli esercizi, proviamo a risolvere insieme la derivata dell’arcoseno del logaritmo. Può sembrare un esercizio difficile ma, come stai per vedere, bastano davvero pochi passaggi per arrivare alla soluzione:
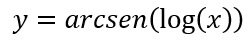
Applichiamo subito la formula vista dove al posto di f(x) mettiamo il log(x) e al posto di f'(x) la derivata del logaritmo, che sappiamo essere pari a 1/x.
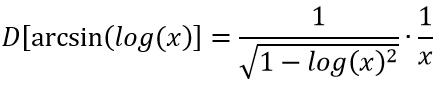
Conclusioni
Non c’è più altro da dire, come hai potuto vedere anche se si tratta di enti matematici che gli studenti trovano difficili (come l’arcoseno o il logaritmo), gli esercizi sono davvero facili una volta capita la regola.
Se questa lezione ti è stata d’aiuto, ti chiediamo di lasciare un commento positivo. Ci aiuterai a migliorare la qualità dele lezioni e a rispondere alla tante domande che ogni giorno ci ponete voi studenti. Buono studio 😉