La derivata di x è una delle operazioni di derivazione più semplici e veloci da eseguire. In questa lezione vedremo qual è la derivata di x e come si dimostra il risultato ottenuto. Senza perderci in troppi indugi, definiamo la funzione di partenza f(x)=x e calcoliamo la sua derivata:
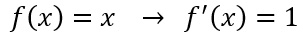
Le regola è molto semplice: la derivata di x è uguale a 1. Essendo una funzione di tipo lineare, cioè visto che il grado del polinomio (in questo caso un monomio, x appunto) è uguale a 1, la derivata prima può essere calcolata applicando la regola delle potenze vista nella tabella delle derivate fondamentali.
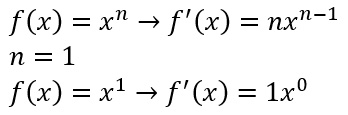
Poiché un numero elevato a 0 fa sempre 1, allora f'(x)=1. Semplicemente quindi servendoci delle derivate immediate, siamo arrivati rapidamente ad una soluzione. Con questo metodo si possono calcolare anche la derivata di una potenza o la derivata di una radice, non cambia assolutamente nulla.
Derivata di x: dimostrazione
Per poter dimostrare il risultato di quest’operazione, ci serviamo del metodo del rapporto incrementale. Quindi definito un incremento h relativo alla funzione f(x)=x, possiamo calcolare il limite:
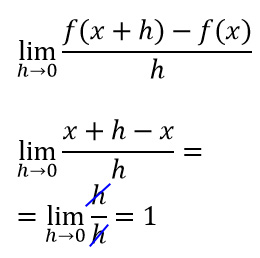
Questo tipo di dimostrazione si applica a tutte le funzioni lineari, quini di primo grado. Non ci credi? Abbiamo calcolato (e dimostrato) anche quanto vale la derivata di 2x.
Conclusioni
Abbiamo visto in questa piccola lezione che la derivata di x vale sempre 1. Non importa il contesto e non c’è bisogno di ragionare tanto: ogni volta che devi calcolare la derivata prima di x hai sempre la certezza che il risultato è 1.
Prima di andare via, ricordati di lasciarci un commento positivo in basso. Ci aiuterà a fornirti ogni giorno delle spiegazioni di qualità e a rispondere alle tante domande che ogni giorno voi studenti ci inviate.