Una delle operazioni di derivazione più semplici, ma allo stesso tempo più sbagliate dagli studenti è la derivata di una costante. Come si calcola la derivata di un numero, che sia positivo o negativo, un intero o una frazione?
In questa guida vedremo quanto vale la derivata di una costante e daremo una dimostrazione utilizzando il metodo del rapporto incrementale. Iniziamo subito definendo una funzione f(x)=k, dove k è un numero appartenente all’insieme dei numeri reali R, allora la sua derivata f'(x) è uguale a 0.

Qual è la derivata di una costante? E’ sempre pari a 0, qualsiasi il numero, che sia positivo, negativo, intero, fratto o sotto radice. La derivata di un numero è sempre 0.
Derivata di una costante – dimostrazione
Per dimostrare quello che abbiamo appena affermato, ricorriamo alla definizione di derivata, quindi calcoliamo il limite per h che tende a 0 del rapporto incrementale della funzione f(x)=k.
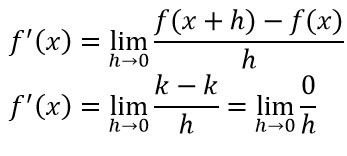
Nel limite appena trovato il numerato è esattamente pari a 0, mentre il denominatore “tende” a 0, ad esempio può assumere un valore pari a 0,0001. Non si tratta quindi del limite di una forma indeterminata, ma il risultato di questa divisione è sempre pari a 0. Da ciò si dimostra che la derivata di un numero (e quindi la derivata di una costante) è sempre zero.
Derivata di una costante – ESEMPIO
Non faremo un esercitazione vera e propria perché c’è davvero poco da dire. Quando hai la fortuna di dover risolvere la derivata di un numero, senza neanche pensarci, sai che il suo risultato è zero! Vediamo un esempio pratico:

Come puoi vedere il risultato è immediato! Lo stesso vale ad esempio se devi risolvere la derivata di zero, la derivata di 1 o la derivata di una frazione: il risultato sarà sempre identico, cioè 0.
Diverso è il discorso in cui devi risolvere la derivata di una costante per una funzione. In tal caso il procedimento è diverso, ma trovi tutte le risposte nella lezione sulle regole di derivazione. Se stai cercando invece una tabella con tutte le derivata con relativa dimostrazione allora vai alla pagina sulle derivate fondamentali.