Conoscere le derivate fondamentali è fondamentale per imparare a risolvere le derivate delle funzioni elementari. Generalmente vengono raccolte nella tabella derivate e applicate durante gli esercizi per poter evitare la risoluzione con il metodo del rapporto incrementale.
Ciascuna delle derivate fondamentali che vedremo tra poco ha una sua precisa dimostrazione, ma generalmente vengono applicate fedelmente senza troppe difficoltà. Vanno imparate a memoria? Si, ma non preoccuparti, le imparerai poco alla volta semplicemente facendo pratica con gli esercizi.
Se hai già studiato la definizione di derivata, se allora pronto per lo step successivo e studiare assieme a noi il formulario delle derivate fondamentali. Eccolo:
| FUNZIONE DA DERIVARE | FUNZIONE DERIVATA |
|---|---|
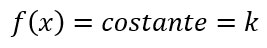 Derivata di una costante | |
Derivata di x | |
Derivata di una potenza | |
Derivata di e alla x | |
Derivata di un esponenziale | |
Derivata del logaritmo | 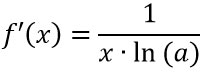 |
Derivata del logaritmo naturale | 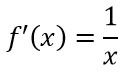 |
Derivata del seno | |
Derivata del coseno | |
Derivata della tangente | 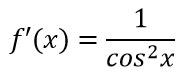 |
Derivata della cotangente | 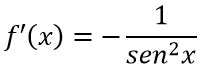 |
Derivata dell’arcoseno | 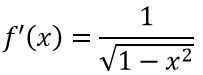 |
Derivata dell’arcocoseno | 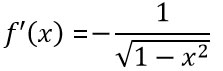 |
Derivata dell’arcotangente | 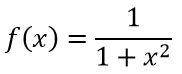 |
Derivata dell’arcocotangente | 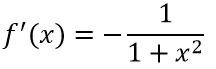 |
Per la dimostrazione delle formule delle derivate immediate clicca sul link all’interno della tabella in corrispondenza della derivata a cui sei interessato. Troverai, oltre alla dimostrazione, anche tanti esempi ed esercizi svolti e commentati.
Intenzionalmente nel formulario non abbiamo inserito la derivata di una radice, perché riteniamo inutile imparare a memoria troppe formule: impariamo solo quello che è indispensabile. In tal caso, semplicemente facendo riferimento alle proprietà delle potenze e alle proprietà dei radicali, si trasforma la radice in un potenza, così a ricondurci alla derivata immediata n.3 vista nella tabella.
Non ti ricordi, come si trasformare una radice in una potenza? Fai riferimento alla seguente formula:
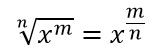
Come si usano le derivate fondamentali?
Le funzioni che hai visto elencate all’interno della tabella in alto ti consentono di risolvere le derivate elementari. Di fronte a problemi più complessi è necessario completare quanto visto fino ad ora aggiungendo due ulteriori nozioni.
Le regole di derivazione
Sono delle formule che consentono di risolvere gli esercizi in cui sono presenti costanti, somme, differenze, prodotti o rapporti con le derivate. Si tratta di poche e semplici regole, ma di fondamentale importanza e che generalmente vengono immediatamente imparate dagli studenti proprio per la loro immediatezza e semplicità.
Le derivate composte
In questa lezione ci siamo occupati delle derivate notevoli, ovvero delle funzioni semplici che permettono di trovare in maniera immediata la soluzione. Come bisogna comportarsi, però, quando ci sono esercizi più complessi come nel caso delle derivate delle funzioni composte?
Abbiamo visto ad esempio come risolvere la formula della derivata immediata del logaritmo, ma come si risolve la derivata del logaritmo che ha come argomento un polinomio o una potenza? Se hai già capito come leggere ed utilizzare le derivate immediate viste in questa tabella hai già fatto il 90% del lavoro. Vedremo infatti che le derivate composte non sono altro che un’estensione delle formule delle derivate elementari.