Che cos’è un polinomio omogeneo? Qual è la sua definizione e come facciamo a capire quando un polinomio è omogeneo? In questa lezione vedremo tutto ciò che c’è da sapere sui polinomi omogenei con definizioni ed esempi svolti.
DEFINIZIONE
Un polinomio omogeneo è tale se tutti i suoi monomi hanno lo stesso grado.
Vediamo in breve cosa significa: ti ricordi la definizione di grado di un polinomio? In quel caso andavamo ad analizzare il grado massimo di ogni monomio. In questo caso, invece, andiamo a verificare che il grado di ogni monomio resti costante.
Come riconoscere un polinomio omogeneo
Dalla definizione di polinomio omogeneo appare evidente che l’unico elemento da prendere in considerazione è il grado di ogni monomio, quindi l’insieme di potenze presenti. Non importa quante e quali lettere sono presenti (Approfondimenti: Equazioni letterali intere e fratte di primo grado – esercizi svolti ) i casi in questo caso sono soltanto due:
- i monomi hanno tutti lo stesso grado, per cui il polinomio è omogeneo;
- i monomi hanno gradi differenti, per cui il polinomio è non omogeneo.
Esempi di polinomi omogenei
ESERCIZIO 1
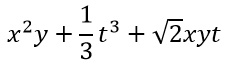
Per verificare che faccia parte dei polinomi omogenei, andiamo a calcolare il grado di ogni monomio. Ad esempio x alla seconda ha grado 3 (la somma degli esponenti 2+1=3). Allo stesso modo il secondo monomio, un terzo t al cubo, è un monomio di terzo grado. Lo stesso si può dire per l’ultimo monomio che ha tutti i termini di primo grado, per cui sommandoli si ottiene grado 3 (1+1+1).
Poiché tutti i monomi sono di grado 3, allora si tratta di un polinomio omogeneo.
ESERCIZIO 2
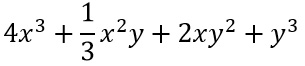
Quello espresso nella traccia è un polinomio omogeneo ordinato e completo rispetto alla lettera x. In questo caso vediamo che il grado di ogni monomio è pari a 3, per cui è omogeneo. Inoltre è completo e ordinato rispetto alla x perché sono presenti tutti i gradi della x in senso decrescente.
ESERCIZIO 3
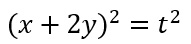
Al primo membro dell’equazione vedi un quadrato di binomio. Dalla sua soluzione si ottiene:
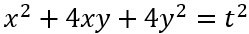
Tutti i monomi hanno grado 2, per cui anche rientriamo nuovamente nella casistica dei polinomi omogenei.
ESERCIZIO 4
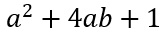
In questo caso mentre i due primi monomi sono di grado 2, il termine noto del polinomio (ovvero +1) è di grado 0. Per cui l’esempio mostra un caso di polinomio non omogeneo.
Conclusioni
Quello dei polinomi omogenei è un argomento un po’ sottovalutato. E’ vero che non ha un riscontro immediato nel programma di algebra, però ti troverai ad utilizzarli in futuro. Un esempio? Le equazioni differenziali omogenee!