In questa lezione ci occuperemo di introdurre il significato di trasformazione geometrica di punto o di una funzione, per passare poi ad un’analisi schematica delle principali trasformazioni geometriche piane con esempi ed esercizi svolti.
Si tratta di un argomento che viene spesso sottovalutato nei programmi di matematica del liceo scientifico, perché si incontrano poche funzioni da trasformare. In fisica, invece, con la teoria dei vettori, si trovano spesso tante similitudini e anche per questo è importante conoscere e riconoscere le principali trasformazioni geometriche nel piano cartesiano.
Ecco l’indice della lezione di oggi:
- Definizione di trasformazioni geometriche
- Equazioni della trasformazione
- Esercizi svolti – trasformazioni di funzioni e di punti
- Composizioni
- Isometrie (traslazione, rotazione, simmetrie)
- Omotetie
- Similitudini
Trasformazioni geometriche definizione
Una trasformazione geometrica è una corrispondenza biunivoca che associa ad ogni punto del piano uno e un solo punto del piano stesso.
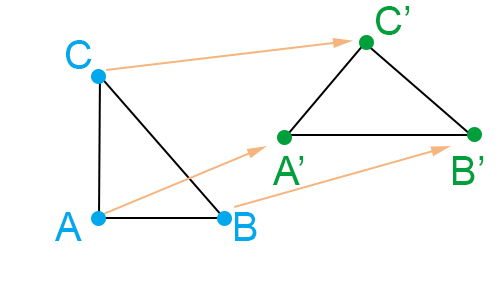
Se indichiamo con t una generica trasformazione geometrica nel piano, per dire che associa a un punto A del piano un altro punto A’ possiamo utilizzare la notazione matematica:
t : A → A’, oppure A’ = t(A)
dove A’ viene chiamato trasformato o immagine di A, mentre A rappresenta l’antitrasformata o controimmagine di A’. Poiché abbiamo parlato di trasformazione biunivoca, allora esiste sempre la trasformazione inversa che si indica con t^-1 (si legge t alla meno 1)
Equazioni della trasformazione geometrica
Dato il piano cartesiano Oxy attraverso delle opportune funzioni possiamo associare ad ogni punto A(x,y) il suo trasformato A'(x’,y’). Queste funzioni si chiamano equazioni della trasformazione e consentono di scrivere le coordinate di A’ in funzione delle coordinate di A.
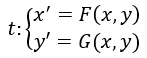
Affinché le due funzioni F e G rappresentino effettivamente delle trasformazioni geometriche è necessario che ci sia corrispondenza biunivoca, cioè è necessario che dalle coordinate (x,y) si possa passare a (x’,y’) e viceversa.
Esempio 1
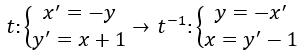
In questo caso la trasformazione associa a ogni coppia (x,y) una sola coppia (x’,y’) e viceversa.
Esempio 2
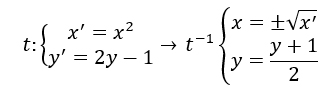
In questo caso non ho una trasformazione geometrica perché se dato x ho un solo valore di x’, dato x’ ho due valori di x. Questo perché per le regole dei radicali devo inserire il segno più/meno.
Esercizio svolto – Trasformare punti
Troviamo l’immagine dei punti A e B applicando la trasformazione geometrica t.
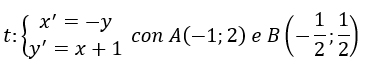
Quindi dai punti A e B, attraverso t, bisogna ricavare A’ e B’. E’ sufficiente sostituire le coordinate x e y di A e di B per trovare x’ e y’ di A’ e B’.
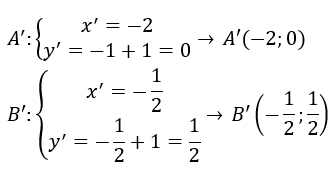
Da notare che B e B’ coincidono. Punti di questo tipo vengono detti punti uniti.
DEFINIZIONE
In una trasformazione geometrica, un punto unito è un punto che ha se stesso per immagine.
Esercizio svolto – Trasformazioni geometriche di funzioni
Quello visto che il generico punto può essere eseguito anche per una generica funzione f(x). Ad esempio consideriamo ancora la stessa trasformazione geometrica t e la funzione f.
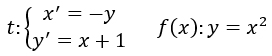
La funzione non è altro che l’equazione della parabola con vertice nell’origine degli assi. Dobbiamo andare a sostituire t all’interno di f(x) per cui mi ricavo x e y dalla parentesi graffa della trasformazione (cioè ricavo l’inversa t^-1):

Dopo aver svolto il quadrato di binomio, abbiamo ottenuto una nuova funzione che possiamo rappresentare sul grafico.
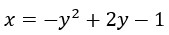
La trasformata geometrica della parabola, in questo caso, è una nuova parabola ma con asse orizzontale.
Composizione di trasformazioni
Supponiamo di voler applicare due trasformazioni geometriche: la prima trasforma P in P1 e la seconda P1 in P2. In questo modo abbiamo ottenuto la trasformazione composta di t1 e t2. Si indica con: t1•t2.
In generale svolgere t1•t2 non è la stessa cosa di t2•t1, per cui non vale la proprietà commutativa. Inoltre per la definizione di trasformazione inversa, è vero che dalla composizione di una trasformazione con la sua inversa si ottiene l’identità: t1•t^-1=1
Isometrie
L’isometria è una delle trasformazioni geometriche nel piano che conserva le distanze. L’isometria trasforma una generica figura in una congruente alla prima, cioè perfettamente sovrapponibili.
DEFINIZIONE
L’isometria è una trasformazione geometrica in cui la distanza tra due punti A e B resta identica anche tra le loro immagini A’ e B’.
In questa lezione vedremo una breve sintesi sulle traslazioni, sulle rotazioni, sulle simmetrie e sulle simmetrie assiali. Per ogni capitolo trovi il link che ti porta alla pagina di approfondimenti in cui, più nel dettaglio, ci occuperemo della trasformazione geometrica con esempi, formule ed esercizi svolti.
Traslazione
Dato un vettore v, la traslazione è la trasformazione geometrica che ad ogni punto P associa un punto P’ tale che PP’=v
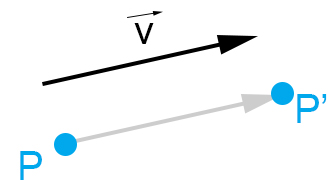
In parole povere la traslazione esegue uno spostamento del generico punto (o della figura). Dal punto P si esegue una traslazione seguendo la direzione di v. Infatti il segmento PP’ ha la stessa lunghezza ed è parallelo a v.
Rotazione
Dati un punto C e un angolo alfa (a), la rotazione di centro C ed ampiezza a è una trasformazione geometrica tale che CP=CP’ e l’angolo PCP’ è congruente ad alfa.
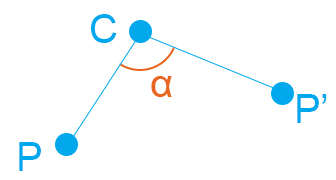
La rotazione viene generalmente indicata con r(C,a). In parole povere, fissato un centro della rotazione, il punto P ruota attorno ad esso di un angolo alfa. Poiché le misure dei segmenti restano invariate, anche questa trasformazione geometrica rientra tra le isometrie. Vedremo nelle lezioni di approfondimento come comportarci con la rotazione rispetto all’origine degli assi cartesiani o rispetto ad un generico punto P.
Simmetria centrale
Fissato un punto M, la simmetria centrale con centro M è la trasformazione geometrica che per ogni punto P del piano fa corrispondere il punto P’, tale che M è il punto medio di PP’.
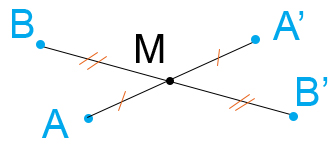
Il punto M è detto centro della simmetria ed è l’unico punto unito. Come puoi vedere dall’immagine, poiché AM=A’M e BM=B’M, allora anche AB=A’B’, per cui anche questa trasformazione geometrica rientra nelle isometrie.
Simmetria assiale
Fissata una retta r, la simmetria assiale associa ad ogni punto P il punto P’ nel semipiano opposto rispetto a r. Inoltre deve valere che r passa perpendicolarmente per il punto medio di PP’.
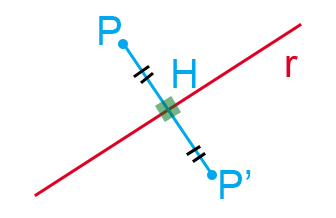
La retta r si chiama asse di simmetria, ricordi che l’abbiamo già incontrata in alcune figure geometriche come la parabola? La simmetria assiale è involutoria, questo vuol dire che facendo la sua trasformazione inversa si ottiene l’identità. In parole povere se provi a “specchiare” ulteriormente il punto P’ ottieni nuovamente P, tornando nella situazione di partenza.
Omotetie
Le omotetie sono delle trasformazioni geometriche che dilatano (aumentando o diminuendo) le misure dei segmenti o dei lati delle figure.
DEFINIZIONE
L’omotetia di rapporto k e centro C è quella trasformazione geometrica che associa a P il punto P’, tale che CP=k⋅CP’
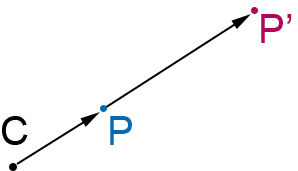
Il punto C è detto centro dell’omotetia mentre k è un numero reale diverso da 0 chiamato rapporto di omotetia. Se k=0 P e P’ stanno sulla stessa semiretta di origine C e l’omotetia si dice diretta. Nel caso in cui k<0 allora i due punti si trovano su due semirette opposte con origine C e l’omotetia si dice inversa. Se |k|>1 allora la figura verrà ingrandita, se -1<k-<1 allora la figura verrà rimpicciolita.
Ad esempio per k=2, la figura risultato della trasformazione sarà due volte più grande. Se k=0,5, allora nuova figura sarà grande la metà rispetto a quella originaria.
Similitudini
Sono simili alle omotetia ma con la differenza che restano costanti il rapporto dei lati. Probabilmente ti ricorderai che nella scuola primaria hai già studiato i criteri di similitudine: ecco questa è la versione “seria” di qualcosa che hai studiato tanti anni fa.
DEFINIZIONE
La similitudine mantiene costante il rapporto tra i segmenti corrispondenti, ossia dati i punti A e B generici e i loro trasformati A’ e B’, si ha che A’B’/AB=k.
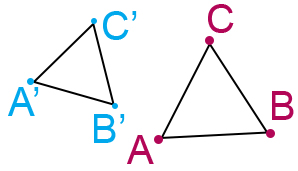
In parole povere le figure simili conservano inalterati gli angoli ma la misure dei lati cambiano. Affinché ciò sia possibile è necessario che il rapporto tra i lati corrispondenti sia costante, cioè AB/A’B’ = BC/B’C’ = AC/A’C’.
Conclusioni
In questa lezione generale sulle trasformazioni geometriche abbiamo visto tutte le tipologie che si studiano generalmente nelle scuole superiori. Le formule puoi trovarle direttamente nella lezione di approfondimento di ciascuna trasformazione, che ti consigliamo di leggere. Troverai tanti esempi, appunti ed esercizi svolti.
Se la lezione di oggi ti è stata utile e l’hai trovata chiara o se hai dei dubbi, lasciaci un commento. Ci aiuterai a migliorare la qualità delle lezioni che ti offriamo ogni giorno! Buono studio 😉