Il punto medio di un segmento è quel punto che divide il segmento in due parti uguali. In geometria analitica esiste una formula molto semplice che permette di calcolare le coordinate del punto medio nel piano cartesiano, noti i due estremi del segmento.
Dopo aver studiato la formula della distanza tra due punti abbiamo imparato a determinare la lunghezza di un generico segmento. In questa lezione vedremo la definizione di punto medio e subito dopo la formula per il punto medio da applicare in tutti gli esercizi di geometria analitica. Infine metteremo in pratica quanto appreso attraverso degli esempi e degli esercizi svolti.
Definizione di punto medio
Dato un segmento di estremi A e B, si definisce punto medio del segmento, quel punto M che divide il segmento in due parti uguali.
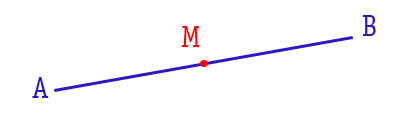
Vale quindi la relazione:
AM=MB
La definizione vista si applica non solo allo spazio bidimensionale (cioè al piano cartesiano), ma anche allo spazio tridimensionale.
ATTENZIONE: è sbagliato parlare di punto medio di una retta. Quest’ultima è infatti un ente geometrico di infinite dimensione per cui è impossibile trovarne la metà. Si parla invece di punto medio del segmento, proprio perché quest’ultimo ha una dimensione finita e compresa tra due punti (detti estremi)
Formula del punto medio nel piano cartesiano
Siano date le coordinate degli estremi del segmento A(xA; yA) e B(xB ; yB) ci sono due semplici formule che permettono di calcolare le coordinate del punto medio M(xM; yM).
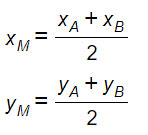
Per calcolare il punto medio tra due punti è sufficiente cioè fare la media delle ascisse e delle ordinate. Anche per questa ragione su alcuni vecchi libri di testo M è indicato come punto mediano.
In base alla formula vista possiamo dire quindi che:
- l’ascissa del punto medio è pari alla semisomma delle ascisse dei due estremi;
- l’ordinata del punto medio è pari alla semisomma delle ordinate dei due estremi.
Formule inverse
Se è noto un estremo e il punto medio del segmento, è possibile calcolare il secondo estremo applicando la formula inversa. Per trovare ad esempio il punto B:
xB= 2xM-xA
yB= 2yM-yA
Se invece hai bisogno di calcolare l’estremo A ti è sufficiente invertire i pedici all’interno della formula, per ottenere quindi:
xA= 2xM-xB
yA= 2yM-yB
Esercizi svolti
Abbiamo capito come si calcola il punto medio o meglio quali sono le formule da usare. Vediamo ora nella pratica come si risolve un problema di geometria che richiede il calcolo di M.
Esercizio 1
Calcolare il punto medio del segmento AB dove le coordinate del punto sono A(1;2) B(3;6).
Per risolvere questo facile problema semplicemente applichiamo le formule viste in questa lezione. Otteniamo quindi il punto M:
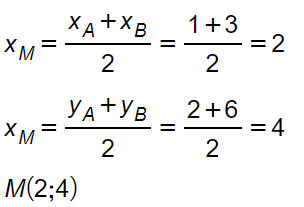
Esercizio 2
Noti i due estremi di un segmento A e B con le coordinate riportate sotto, determinare il punto medio.

Esercizi da risolvere
Ora prova tu a risolvere i seguenti esercizi ricordandoti la lezione sulla distanza tra due punti. Determina la distanza e il punto medio tra le seguenti coppie di punti:

Come sempre lo staff di Esercizimatematica.com siamo a vostra disposizione per dubbi o chiarimenti sulla lezione di oggi (Contattaci) Se invece ti è tutto chiaro puoi passare direttamente alla prossima lezione e finalmente iniziare a studiare l’equazione della retta.