La scomposizione di un cubo di binomio avviene a partire da un quadrinomio in un cui sono facilmente riconoscibili due termini con la terza potenza o di cui è facilmente eseguibile la radice cubica.
La formula è la stessa che abbiamo già visto per il sviluppo del cubo di binomio, ma primo e secondo termine sono invertiti.
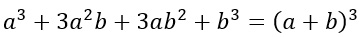
Spiegazione
Nelle precedenti lezioni ci siamo occupati del calcolo dei prodotti notevoli, ovvero di quelle operazioni algebriche ci semplificano gli esercizi permettendoci di saltare diversi passaggi con poche e semplici regole.
Siamo partiti dalle formule più semplici come il quadrato di binomio fino ad arrivare ad operazioni più complesse come il cubo di trinomio. Tutte queste regole possono essere utilizzate anche per le scomposizioni di polinomi semplicemente capovolgendo la formula, cioè invertendo primo e secondo membro.
Cubo di binomio scomposizione
La scomposizione del quadrinomio viene considerata tra le più difficili per una sola ragione. E’ difficile non da applicare ma da riconoscere.
Cioè una volta che abbiamo 4 termini, come facciamo a capire che si tratta di un cubo di binomio?
Ecco cosa suggerisco ai miei studenti:
- Verifica che nel polinomio da scomporre ci siano effettivamente 4 termini.
- Verifica che ci siano due monomi che siano dei cubi. Quindi o troverai direttamente la potenza con indice 3 oppure troverai un numero di cui è agevole calcolare la radica cubica: ad esempio 8 o 27 sono la radice cubica di 2 e 3 rispettivamente.
- una volta trovati i due cubi, prova con loro a svilupparti su un foglio da parte il cubo del binomio. Se il quadrinomio che ottieni è uguale a quello di partenza allora la scomposizione può avvenire.
Ci hai capito poco? Lo so, è normale, tranquillo! Ora vediamo subito degli esempi per rendere tutto più chiaro e vedrai che è più facile da fare che da spiegare.
Esercizi svolti
Esempio 1
Proviamo a scomporre insieme il seguente polinomio.
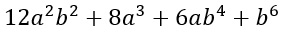
Il primo passo è quello di riconoscere che il quadrinomio sia effettivamente riducibile al cubo del binomio.
- Individuiamo – sempre che siano presenti! – i due monomi al cubo. In questo caso abbiamo 8a alla terza e b alla sesta. Calcolando infatti la radice cubica di entrambi ottengo 3a e b al quadrato. ✔️
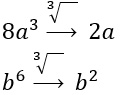
- Utilizziamo ora questi due monomi appena individuati per sviluppare da parte il cubo. Visto che i segni sono entrambi positivi, restano positivi.
NB: ricorda che il cubo mantiene i segni. Se uno di questi due termini fosse stato col segno meno nel quadrinomio di partenza, avremmo mantenuto il segno meno anche nel binomio da elevare al quadrato.
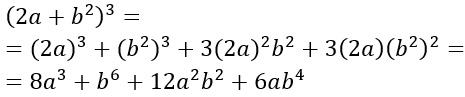
- Poiché il quadrinomio ottenuto è identico a quello di partenza (non badare al fatto che i termini hanno una posizione diversa, non cambia nulla), allora può essere eseguita la scomposizione:
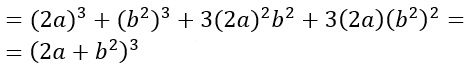
Esempio 2
Esegui la scomposizione del quadrinomio seguente:
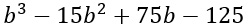
L’unica grossa differenza dall’esercizio precedente su cui prestare attenzione è la presenza di segni negativi.
- Individuiamo subito i termini al cubo. Notiamo che b alla terza è il cubo di b, mentre 125 è il cubo di 5. ✔️
- Mantenendo i segni, il nostro binomio sarà quindi: (b-5). Occorre solo verificare che i termini intermedi corrispondano nel calcolo del cubo di binomio. Sviluppiamoci quindi da parte il binomio b-5 elevandolo alla terza.
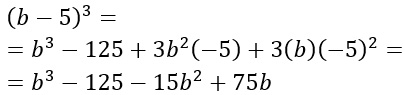
Puoi notare che il quadrinomio ottenuto coincide con quello di partenza, per cui quest’ultimo può essere scomposto come:
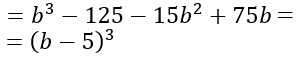
Conclusioni
Abbiamo visto come la scomposizione di un cubo di binomio avviene sostanzialmente attraverso due passaggi: si individuano i termini alla terza e con questi si sviluppa un cubo di binomio come prova. Basta un solo segno o un numero che non corrisponda con la traccia e l’operazione di scomposizione non può avvenire.
Se questa lezione ti è stata utile, ti invitiamo a lasciare un commento o un feedback positivo in basso. Ci aiuterai a crescere e a fornirti ogni giorno delle lezioni di qualità. Buono studio 😉