Il teorema di unicità del limite è una dei teoremi che sta alla base dello studio dei limiti in matematica ed assicura che, data una funzione f(x), se esiste il suo limite per x->x0, allora questo è unico.
In parole povere, quando si va a calcolare un limite non è possibile avere un doppio risultato. Ti ricordi cosa accadeva con le equazioni di secondo grado? Partendo da una singola equazione, con la formula del delta, avevi due risultati. Il teorema dell’unicità del limite dimostra che il risultato è necessariamente unico.
Enunciato
Sia f(x) una funzione con limite finito in l per x->x0, allora tale limite è unico.
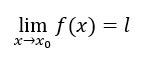
Teorema unicità del limite dimostrazione
Per poter dimostrare questo teorema dobbiamo aver già studiato la definizione di limite e faremo una dimostrazione per assurdo. Significa che ipotizzeremo che la condizione contraria a quella esposta dal teorema, per dimostrare che questa è assurda, ovvero impossibile.
Il teorema di unicità del limite si dimostra per assurdo, per cui iniziamo ammettendo che il limite non sia unico, anzi ne esistano due diversi per la stessa funzione.
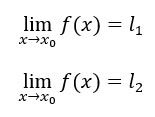
Essendo due limiti differenti, vuol dire che che l1 è diverso da l2, ad esempio ipotizziamo che l1<l2, ovvero che il risultato del primo limite sia minore del risultato del secondo limite.
A questo punto utilizziamo la definizione di limite, te la ricordi? Eccola:
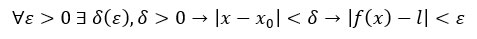
Nella definizione di limite si inizia con “per ogni epsilon (ε) maggiore di 0”. Questo vuol dire che posso scegliere un valore arbitrario, cioè qualsiasi a mia scelta, l’importante è che sia positivo.
Scelgo quindi:
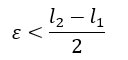
Posso applicare quindi la definizione ai due limiti che ho ipotizzato per assurdo:
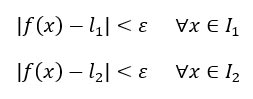
Nella seconda parte trovi “per ogni x appartenente all’intorno I1 e I2 di x0″. Osservo ora che l’intersezione di I1 e I2 è sempre un intorno di x0, per cui devono valere entrambe le due disequazioni in valore assoluto che ho appena scritto. Questo vuol dire che possono scriverle come sistema e sviluppare il valore assoluto:
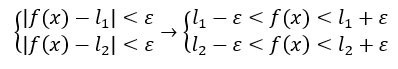
Proviamo a guardare meglio le due disequazioni scritte e prendiamo in considerazione solo le condizioni evidenziate. Possiamo unirle e scrivere direttamente che f(x) deve essere maggiore di l2-ε e minore di l1+ε
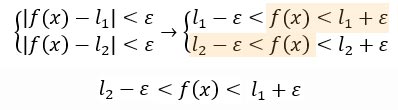
Se l1+ε è maggiore di f(x) che a sua volta è maggiore di l2-ε, vuol dire che vale:
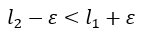
In questa disequazione ottenuta, porto epsilon al primo membro e i valori dei limiti 1 e 2 al secondo membro.
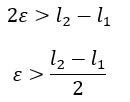
L’ultima disequazione a cui siamo pervenuti è assurda perché contraddice le ipotesi che avevamo fatto all’inizio. Se torni qualche riga più in alto, noti infatti che abbiamo supposto che epsilon sia minore della semidifferenza dei due limiti, mentre come risultato abbiamo trovato che epsilon è maggiore. Quindi è assurdo!
Questo vuol dire che data la funzione f(x), se il suo limite esiste ed è finito, questo è unico.
Validità del teorema di unicità del limite
La dimostrazione che abbiamo appena visto, l’abbiamo applicata al limite finito che tende a valore finito. Tuttavia si dimostra che la validità del teorema di unicità del limite è applicabile anche per le altre tipologie di limiti (infinito e/o tendente ad inifinito)
Conclusioni
Il teorema dell’unicità del limite, come è stato possibile intuire, non è particolarmente complesso ma è di fondamentale importanza nel programma di analisi perché è il punto di partenza per numerosi altri teoremi di cui parleremo in seguito.
Per qualsiasi dubbio o chiarimento il nostro staff resta è a tua disposizione. Lascia un commento o un feedback in basso, ci aiuterà a migliorare ogni giorno la qualità delle lezioni che trovi su questo sito.