L’elevamento a potenza è un’operazione matematica che viene utilizzata quando un numero a viene moltiplicato per se stesso n volte.
In questa guida vedremo tutto quello che c’è da sapere sul calcolo dell’elevamento a potenza, dalle regole da seguire ai casi particolari con le frazioni o con i numeri negativi.
Come si rappresenta l’elevamento a potenza
L’elevazione a potenza viene matematicamente rappresentata attraverso due numeri.

Il numero a viene definito base della potenza, mentre il numero n si chiama esponente. Vedremo tra un istante il significato di questi due termini.
CONSIGLIO: “si legge a alla enne”
L’esponente viene indicato all’apice del numero, mentre potrebbe capitarti di trovare su computer e strumenti informatici il simbolo ^.
Ad esempio 2^3 significa 2 elevato a 3 e si legge 2 alla 3.
Come si leggono le potenze (al quadrato e al cubo)
Generalmente l’elevamento a potenza si legge nel seguente modo:
“numero di base” ALLA “numero dell’esponente”
Ad esempio
- 4^5 si legge 4 alla 5
- 3^2 si legge 3 alla 2
Quando l’esponente è 2 si può leggere anche come:
“numero di base” al quadrato
Ad esempio:
- 3^2 si legge 3 al quadrato
- 5^2 si legge 5 al quadrato
Quando l’esponente è 3 si può leggere anche come:
“numero di base” al cubo
Ad esempio:
- 3^3 si legge 3 al cubo
- 5^3 si legge 5 al cubo
Che significare elevare a potenza?
Immaginiamo di dover risolvere una moltiplicazione. Si voglia, ad esempio, moltiplicare il numero 3 per se stesso 4 volte. Quindi dal punto di vista aritmetico dovremmo scrivere:
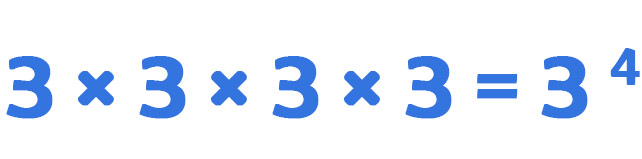
Poiché il numero 3 si moltiplica per 4 volte per se stesso, allora quel numero 4 diventa l’esponente della potenza, mentre il 3 diventa la base.
Quindi che cosa sono le potenze?
Elevare a potenza significa moltiplicare un numero (detto base) un certo numero di volte n (detto esponente) per se stesso.
Esempio: 2^5 → il numero 2 viene moltiplicato 5 volte: 2×2×2×2×2
Volendo semplificare al massimo, possiamo dire che le potenze sono delle moltiplicazioni ripetute di uno stesso numero.
Esempio: elevare al cubo il numero 2. → 2^3=2×2×2=8
Elevamento a potenza – casi particolari
Di seguito vediamo alcuni utili consigli da applicare agli esercizi ed alcune “potenze particolari” che possono essere risolte in maniera più semplice e veloce.
Come si risolve se la base è una frazione?
Le frazioni con potenze mettono spesso in difficoltà gli studenti, ma in realtà sono estremamente semplici. Bisogna solo fare attenzione e chiedersi se l’esponente si riferisca a tutta la frazione, solo al numeratore o solo al denominatore. In tal senso sono utilissime le parentesi.
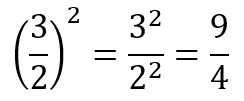
Come risolvere una potenza con esponente fratto?
Nel caso in cui la frazione sia presente all’esponente, si esegue la trasformazione in radicali. Ecco come si risolve in maniera semplice:
- il denominatore dell’esponente diventa indice di radice
- il numeratore dell’esponente diventa esponente
Esempio:
![]()
Il 3 è diventato l’indice della radice, mentre il due ha trasformato la base in una potenza al quadrato.
Che succede se l’esponente è 0?
Se la base è diversa da zero, qualsiasi numero elevato a 0 dà come risultato 1. Vediamo un esempio di potenza alla zero.
![]()
Esempio:
- 2^0 = 1
- (1/3)^0 = 1
Che succede se la base della potenza è negativa?
Capita molto spesso negli esercizi di algebra, in cui non si lavora più con i numeri naturali, ma con quelli relativi, razionali o irrazionali.
* se sei uno studente delle scuole elementari vai direttamente al paragrafo successivo, perché i numeri negativi non fanno parte del tuo programma.
La parte numerica non subisce alcuna variazione dal punto di vista dei calcoli. Bisogna solo fare attenzione ai segni. In particolar modo:
- se l’esponente è pari, allora il segno è sempre +
Esempio: (-3)^2 = 9 - se l’esponente è negativo, allora il segno si conserva, cioè se la base ha segno “meno” resta “meno”. Se ha segno “più” resta “più”
Esempio: (-3)^3 = -27
Che succede se l’esponente è negativo?
Nel caso in cui ci sia una potenza negativa, cioè elevamento a potenza con esponente negativo, allora si trasforma la base: si invertono numeratore e denominatore (se non c’è è sottinteso 1) e a quel punto si può togliere il meno dall’esponente.
Ad esempio:
- 2^(-2) = (1/2)^2 = 1/4
- (2/3)^(-2) = (3/2)^2 = 9/4
Quindi le potenze ad esponente negativo se elevano semplicemente con 1 passaggio matematico in più.
Proprietà delle potenze
In questa lezione ci siamo occupati esclusivamente delle regole base sull’elevamento a potenza. Per poter eseguire dei calcoli con le operazioni principali è fondamentale a questo punto passare a studiare la lezione successiva, cioè le proprietà delle potenze.
Se invece stai cercando degli esercizi, ti consigliamo la nostra lezione sulle espressioni con le potenze o sugli esercizi con le potenze.