Il decagono è la figura geometrica composta da 10 lati e 10 angoli. Si parla invece di decagono regolare quando il poligono ha gli angoli e i lati congruenti.
In questa lezione vedremo tutte le caratteristiche del poligono regolare, dato che per quello generico non esistono formule specifiche. Vedremo come calcolare l’area, quali sono il numero fisso e la costante d’area e faremo alcuni riferimenti anche alla costruzione del decagono regolare, che si studia in genere nei programmi di disegno tecnico delle scuole medie.
La prima domanda che ci pongono gli studenti è quanti lati ha un decagono? Per rispondere a questa domanda vediamone subito la definizione.
Definizione
Il decagono è un poligono con dieci lati ed è regolare nel caso in cui questi sono tra loro congruenti.
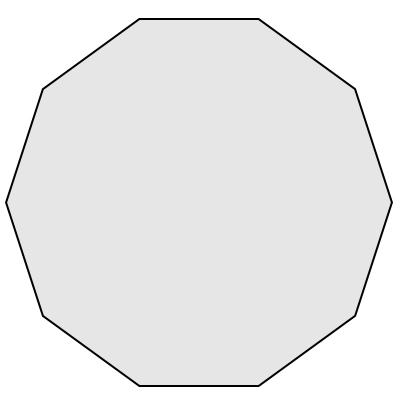
Nell’immagine sopra, abbiamo disegnato il decagono regolare. Infatti il poligono ha 10 lati tutti uguali e 10 angoli uguali.
Decagono formule
Rispetto agli altri poligono regolari visti, il discorso è perfettamente analogo. Esistono due costanti che permettono di calcolare l’apotema e l’area a partire dal lato.
Numero fisso f=1,539
E’ un numero che resta costante in tutti i decagoni regolari, indipendentemente dalla misura dei lati. Si ottiene attraverso il rapporto tra apotema e lato.
Costante d’area Φ=7,694
Così come il numero fisso, la costante d’area è un numero che resta sempre uguale indipendentemente dalla misura del lato. E’ utile per calcolare l’area del decagono dato il lato.
Perimetro del decagono regolare
Visto che il perimetro è la somma di tutti i lati e il decagono ne ha 10 tutti uguali, è sufficiente conoscere un lato e moltiplicarlo per 10. Quindi la formula da usare è:
p=10·L
Area decagono
Il modo più semplice per calcolare la superficie di questa figura è utilizzare la misura del lato. Conoscendo la costante d’area (Φ=7,694), è possibile scrivere:
A=Φ·L²
Esistono altre formule che permettono di effettuare i calcoli nel caso di decagono inscritto in una circonferenza (o circoscritto). Tuttavia vengono utilizzate così raramente che evitiamo di includerle in questa lezione. Potrete eventualmente richiederle nei commenti, se necessario.
Proprietà del decagono regolare
- La figura può essere sia inscritta che circoscritta all’interno di una circonferenza.
- La somma degli angoli interni (180·N-360)=1.440°.
- Ogni angoli misura 144°.
- Le diagonali di un decagono sono 35 e per ogni vertice partono 7 diagonali.
- Questa figura geometrica ha 10 assi di simmetria.
- Il centro del decagono è centro di simmetria.
Costruzione decagono regolare
Veniamo alla parte più pratica e applicativa che riguarda il disegno. Per costruire un decagono regolare puoi seguire questo tutorial.
Costruzione decagono data la circonferenza
- Disegniamo la circonferenza di centro O
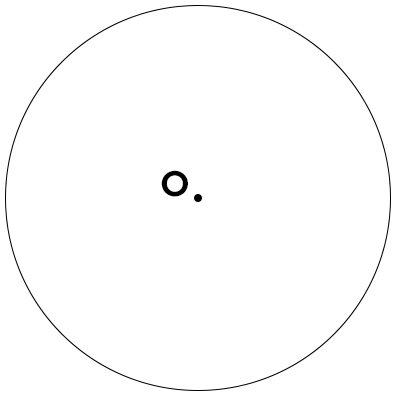
- Traccio i due diametri (orizzontale e verticale e li chiamo 1-2 il primo e AB il secondo)
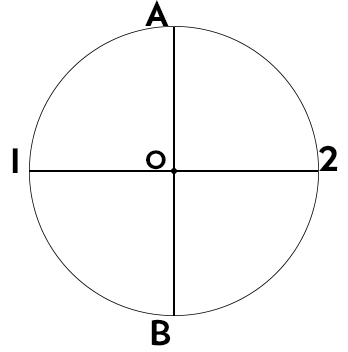
- Apertura di compasso pari ad AO, cioè al raggio, si punta in 1 e si disegna un arco per individuare i punti 3 e 4.
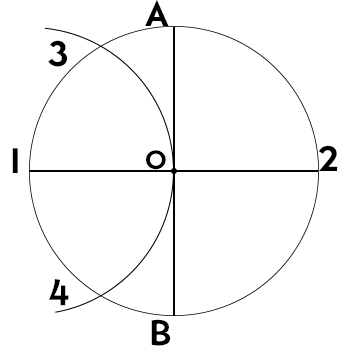
- Congiungiamo i punti 3 e 4 per trovare il punto 5 sul diametro orizzontale.
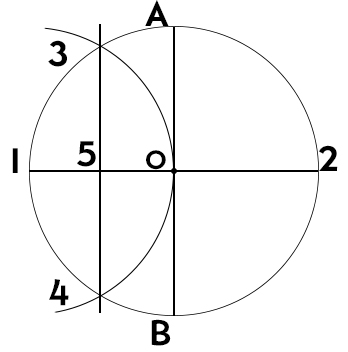
- Con apertura 5-O, centro in 5, si traccia una circonferenza. Si uniscono i punti 5-A e si trova il punto 6 sulla circonferenza appena tracciata.
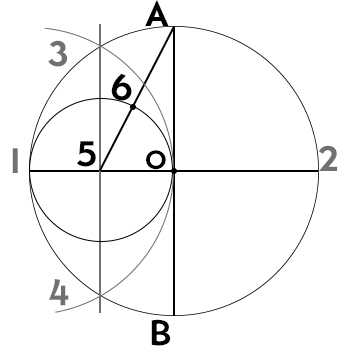
- Consideriamo il segmento A-6. Apriamo il compasso di questa misura e disegniamo sulla circonferenza grande il punto C.
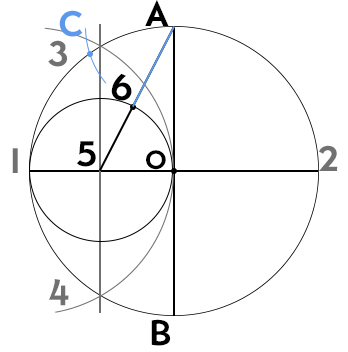
- A questo punto, con la stessa apertura, puntiamo il compasso in C per ottenere D, poi E, poi F… Fino ad ottenere il decagono completo.
Decagono esercizi
Esercizio 1
Calcolare perimetro e area del decagono di lato pari a 10 cm.
Svolgimento
Il perimetro si calcola molto semplicemente moltiplicando la misura del lato per 10.
p = 10 · 10 cm = 100 cm
Per il calcolo dell’area, invece, utilizziamo la costante d’area Φ=7,694
A = Φ · (10 cm)² = 7,694 · 100 cm² = 769,4 cm²
Esercizio 2
Calcolare il lato del decagono con area 155 cm²
Svolgimento
In questo caso utilizziamo la stessa formula dell’esercizio precedente, ma nella sua forma inversa. Ricaviamo quindi subito la formula inversa dall’area:
A = Φ · L² → L =√ (A/ Φ)
Eseguiamo ora i calcoli utilizzando i dati forniti dalla traccia.
L=√(155/7,694)= 20,14 cm
Conclusioni
In questa lezione abbiamo approfondito tutte le principali tematiche che riguardano il decagono regolare. Abbiamo visto le formule (e ricavato quelle inverse) e la loro applicazione negli esercizi, facendo anche un mini-tutorial sulla costruzione di questo poligono regolare.
Se la lezione di questa pagina ti è stata utile e l’hai trovata chiara, lascia un commento positivo nei commenti. Ci aiuterai a crescere e a migliorare ogni giorno la qualità dei contenuti.