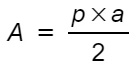L’ottagono è un poligono con 8 lati e 8 angoli. Si parla invece di ottagono regolare quando tutti gli otto lati e gli otto angoli sono uguali tra loro.
In questa guida vedremo alcuni utili approfondimenti per imparare come si fa la costruzione dell’ottagono, quali sono le sue proprietà e le formule da usare negli esercizi.
Che cos’è l’ottagono
Prima di vedere la definizione di questa figura geometrica piana, analizziamo la parola così da capire da dove deriva.
Significato ed etimologia
La parola ottagono è la composizione di due parole greche:
- otta… = okto che significa otto
- …gono = gonia che significa angolo
Definizione
In base a quanto appena visto possiamo dire che l’ottagono è per definizione quella figura geometrica formata da 8 angoli. In genere sui libri di testo si legge che:
l’ottagono è il poligono con 8 lati
Come detto all’inizio di questa lezione, quando i lati sono tutti uguali allora si parla di ottagono regolare.
Proprietà
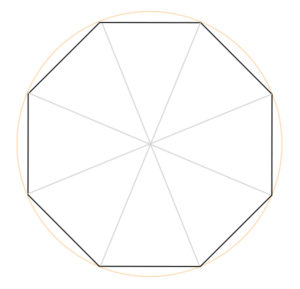
- Dividendo l’ottagono regolare in spicchi, come in figura sopra, si ottengono 8 triangoli isosceli.
- L’angolo al vertice di ogni triangolo è 360°:8= 45°. Per cui, poiché la somma degli angoli interni di un triangolo è 180°, gli angoli alla base sono: (180°-45°):2=67,5°.
- L’ottagono regolare può essere sia inscritto che circoscritto in una circonferenza.
- Apotema ottagono: è il segmento che congiunge il cerchio inscritto con un lato del poligono.
- Il centro del poligono che si ottiene intersecando le diagonali coincide con il centro della circonferenza inscritta e circoscritta.
Formule ottagono regolare
Come in tutti i poligoni regolari esistono due coefficienti che permettono di calcolare l‘area dell’ottagono e l’apotema noto il lato.
Numero fisso ottagono e apotema
Si indica con la lettera f ed è il rapporto tra apotema e lato. E’ una costante e cambia a seconda della figura geometrica considerata. Il numero fisso dell’ottagono è:
f = 1,207
Quindi per calcolare l’apotema dell’ottagono basta moltiplicare il lato per il numero fisso.
a= 1,207 L
Costante d’area
E’ un numero che dipende dal tipo di figura. Si tratta di una costante che mette in relazione il quadrato del lato con l’area del’ottagono.
φ = 4,282
Perimetro ottagono
E’ sicuramente il calcolo più semplice da fare se si conosce il lato. Essendo infatti un poligono regolare, è sufficiente moltiplicare il lato per 8.
p = 8 L
Area ottagono
La superficie di questo poligono regolare può essere calcolata usando due formule a seconda dei dati a disposizione.
- Se sono noti l’apotema e il perimetro:

Si moltiplica il perimetro per l’apotema e si divide il risultato per 2. - Se è noto il lato
A = φ · L²
Si moltiplica il lato al quadrato per il coefficiente d’area dell’ottagono.
Costruzione dell’ottagono (dato il lato)
Vediamo come si costruisce un ottagono regolare utilizzando matita, squadre e compasso.
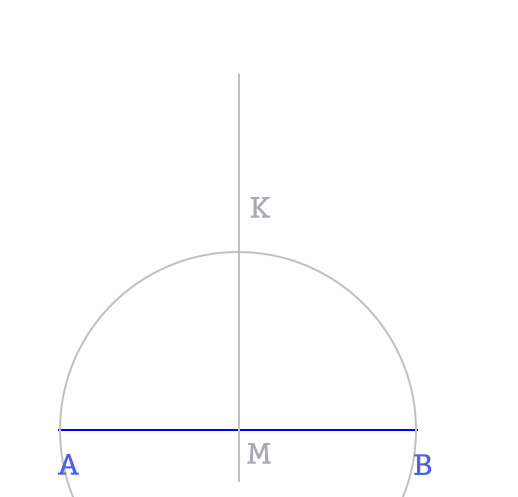
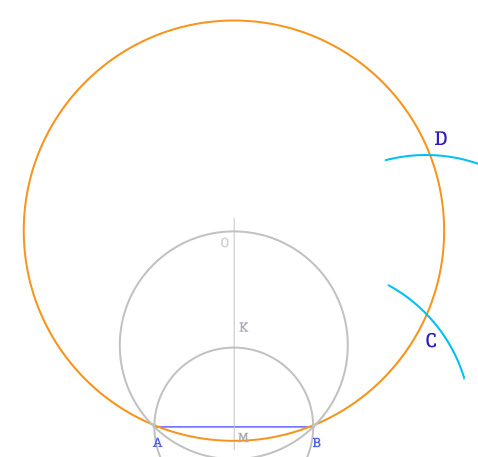
- Iniziamo disegnando il lato AB alla base della figura e la perpendicolare che passa per il punto medio M.
- Con il compasso punto in M, apertura AM, disegno la semicirconferenza individuando il punto K.

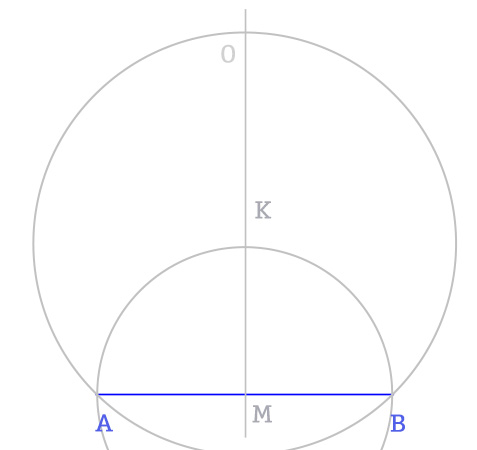
- Punto il compasso su K, apertura AK e trovo il punto O sull’asse del segmento AB.

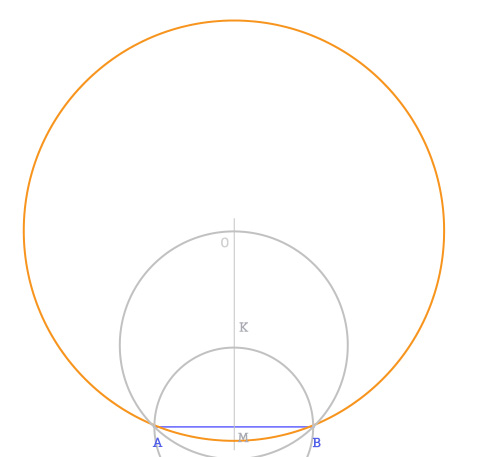
- Puntando in O, apertura del compasso OA, possiamo disegnare ora la circonferenza circoscritta all’ottagono regolare.

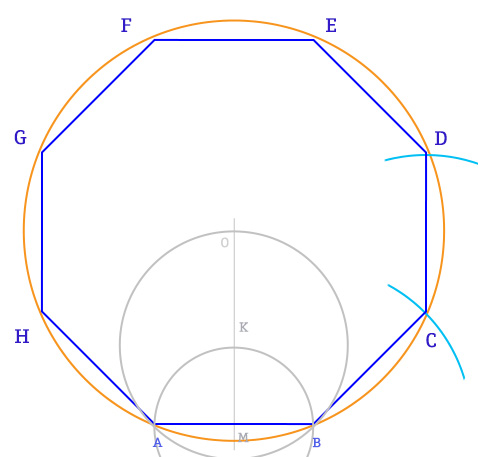
- A questo punto punto in B, apertura AB e inizio a disegnare sulla circonferenza il punto C. Stessa apertura, punto in C e ottengo D e così via…

- Tracciando tutti i punti sulla circonferenza otterremo quindi:

Esercizio
Dato l’ottagono regolare di lato pari a 10 cm, calcolare perimetro e area.
Svolgimento
Il perimetro si calcola semplicemente moltiplicando la misura del lato per 8, cioè per il numero dei lati.
p=10 cm · 8 = 80 cm
L’area dell’ottagono, avendo il lato a disposizione, si può calcolare usando la costante d’area. Per cui possiamo scrivere:
A = φ · L² = 4,282 · 10² = 428,2 cm²