Ellisse formule ed equazioni – il formulario completo

In questa pagina vedremo uno schema completo con tutte le formule dell’ellisse, dalla definizione delle forma canonica sino alle formule più complesse per le traslazioni. Vedremo come si calcolano eccentricità, formule, vertici in caso sia di ellisse orizzontale che verticale.

Nella lezione di introduzione all’ellisse abbiamo già visto nel dettaglio tutta la parte teorica. Abbiamo visto che cosa sono eccentrità, assi di simmetria e fuochi. Lo scopo di questa lezione è fare una sintesi completa che raccoglie in un’unico formulario tutte le equazioni e le formule dell’ellisse.

Formule ellisse con i fuochi sull’asse x

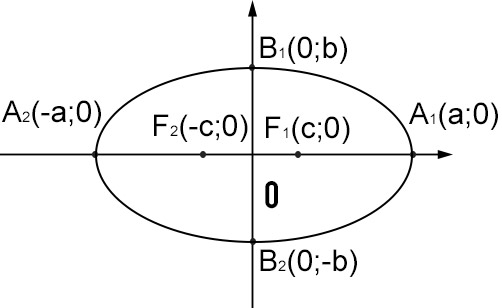
Equazione canonica o normale

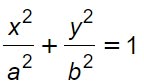
dove a>b e b²=a²-c²

Vertici

A₁(a;0) A₂(-a;0) B₁(0;b) B₂(0;-b)

Lunghezza asse maggiore

A₁A₂=2a

Lunghezza asse minore

B₁B₂=2b

Fuochi

F1(c;0) F2(-c;0) con c>a

Formula eccentricità

e=c/a
dove 0<c<1

---

Formule ellisse con fuochi sull’asse y

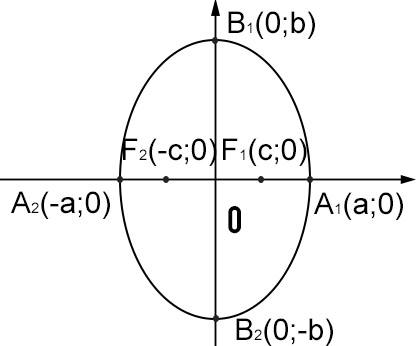
Equazione canonica o normale

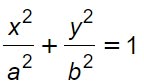
dove b>a e b²=a²-c²

Vertici

A₁(a;0) A₂(-a;0) B₁(0;b) B₂(0;-b)

Lunghezza asse maggiore

B₁B₂=2b

Lunghezza asse minore

A₁A₂=2a

Fuochi

F1(0;c) F2(0;-c) con c>b

Formula eccentricità

e=c/b
dove 0<c<1

Alcuni approfondimenti sulle formule dell’ellisse

Così come la circonferenza, la formula dell’ellisse è di tipo quadratico. Entrambe le incognite compaiono con l’esponente 2, ma a differenza della circonferenza hanno un coefficiente diverso. Inoltre non sono presenti termini di primo grado o termini misti come xy, per cui la figura è sempre simmetrica rispetto ai suoi due assi perpendicolari.

Altra caratteristica in comune con la circonferenza è che la formula dell’ellisse canonica è un’equazione che non rappresenta una funzione. Ti ricordi la definizione di funzione? … ad ogni valore di x si associa uno e un solo valore di y. Se provi a guardare il grafico dell’ellisse e tiri una linea verticale all’interno della figura, ti renderai conto che ci sono due punti di intersezione. Cioè per un valore di x ci sono due valori di y differenti, per cui l’equazione dell’ellisse non è una funzione.

Le formule dell’ellisse sono diverse a seconda che i fuochi si trovino sull’asse delle x o su quello delle y. Nel primo caso la figura avrà un’estensione orizzontale all’interno del piano cartesiano. Nel secondo caso sarà disposta in modo verticale, cioè con l’asse maggiore parallelo all’asse delle ordinate.

La figura ha 4 vertici che corrispondono alle intersezioni con gli assi, simmetrici tra loro rispetto proprio rispetto agli assi.

Per quanto riguarda infine l’eccentricità dell’ellisse, è questo un parametro che misura lo schiacciamento della figura geometrica rispetto agli assi. Più l’eccentricità è bassa e più la figura tende a schiacciarsi. I due casi estremi sono:

• e=0 → l’eccentricità è nulla, per cui l’ellisse degenera in un segmento.
• e=1 → l’eccentricità è massima, per cui l’ellisse degenera in una circonferenza.

Formule ellisse traslata

Data l’ellisse γ, applichiamo a questa la traslazione di vettore v(x0;y0), otteniamo la figura:

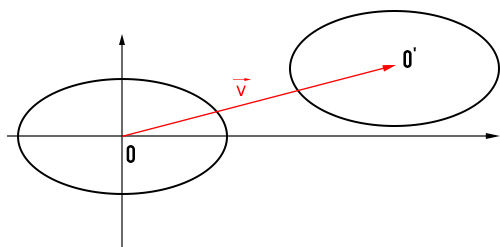
La nuova curva γ0 è un’ellisse avente il centro O'(x0;y0) e assi di simmetria paralleli agli assi cartesiani e di equazioni rispettivamente x=x0 e y=y0. La formula dell’ellisse traslata è l’equazione:

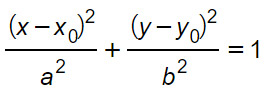
Vertici

A₁(x₀+a;y₀) A₂(x₀-a;y₀) B₁(x₀;y₀+b) B₂(x₀;y₀-b)

Fuochi

se a>b → F1(x₀+c;y₀) F2(x₀-c;y₀) con c²=a²-b²

se b>a → F1(x₀;y₀+c) F2(x₀;y₀-c) con c²=b²-a²