Benvenuto nella lezione sugli esercizi sui radicali. Dopo aver studiato le varie lezioni teoriche è il momento di esercitarsi a risolvere i radicali con esercizi svolti e commentati.. All’interno di questa esercitazione troverai lo svolgimento completo, il commento per i vari passaggi e infine la soluzione.
Ovviamente per essere in grado di risolvere esercizi sui radicali è fondamentale conoscere le regole e le proprietà dei radicali. Se hai ancora dei dubbi non solo sulla teorie e le formule, ma anche su gli esercizi con le radici, ti consigliamo i seguenti approfondimenti:
- Somma di radicali – come si fa l’addizione tra radici?
- Moltiplicazione tra radicali – come si fa il prodotto di due radici?
Esercizi sui radicali svolti
Gli esercizi con le radici che stiamo per risolvere assieme sono ordinati in modo da aumentare il grado di difficoltà in maniera progressiva. Inizieremo da quelli più semplici, quasi banali, per arrivare poi a risolvere esercizi con radicali più complessi.
Esercizio 1
Calcolare le seguenti radici riportando eventualmente i vari passaggi.
√64 3√125 √81 √121 3√1.000
Svolgimento
Questi semplici esercizi sulle radici potrebbero essere risolti in pochi istanti attraverso l’uso di una calcolatrice. Tuttavia, almeno per questi primi esercizi, i radicali verranno risolti a mente. In questo modo potrai capire anche il ragionamento che porta alla risoluzione del problema matematico.
√64
Poiché 8×8=64, allora possiamo scrivere che √64= 8.
3√125
Poiché 5×5×5=125, allora possiamo scrivere che la radice cubica 3√125=5.
√-81
ATTENZIONE: si tratta di una radice quadrata con un numero negativo! Quando l’indice è pari, come in questo caso, la radice negativa è impossibile. Quindi non esistono soluzioni reali.
√121
Poiché 11×11=121, allora posiamo scrivere che √121=11.
3√-1.000
Essendo la radice ad indice dispari, è consentito l’uso dei numeri negativi. Poiché inoltre 10×10×10=1.000, allora 3√-1.000=-10.
Esercizio 2
Risolvere la seguente radice sesta 6√729.
Svolgimento
Dovendo risolvere tutto a mente senza l’aiuto della calcolatrice, proviamo a calcolare la seguente radice scomponendo il numero 729.
729 → 729:3 = 243 → 243:3=81 → 81:3=27 → 27:3=9 → 9:3=3 → 3:3=1
Abbiamo diviso 729 per 3 ben 6 volte. Per cui possiamo scrivere che:
729=3×3×3×3×3×3
729=36
Facendo a questo punto la radice otteniamo:
6√36
La radice e la potenza si semplificano per cui 6 e 6 vanno via e restano 1 e 1. Quindi il risultato finale è 3.
Esercizio 3
Risolvere il seguente esercizio con radicali letterali
4√(81 x8 y4)
Svolgimento
Le radici sono da risolvere in maniera analoga all’esercizio precedente. L’unica differenza è che questa volta ci sono anche delle lettere. Scomponiamo quindi il problema in 3 parti:
- la radice del numero → 4√81 = 4√34 =3.
- la radice della x → 4√x8 = x2 → Abbiamo semplificato 8 e 4 per ottenere 2 come esponente della potenza.
- la radice della y → 4√y4 = y → Abbiamo semplificato 4 e 4, così che spariscono sia la radice che l’esponente.
Ricomponiamo il monomio, per ottenere il risultato finale.
4√(81 x8 y4) = 3x2y.
Esercizio 4
Risolvere la seguente espressione con i radicali
√32+√200
Svolgimento
Ti ricordi cosa abbiamo detto sulle operazioni con le radici? Le somme non si possono fare, o almeno non così facilmente. Visto che non possiamo addizionare, l’unica cosa che possiamo fare in questo caso è fare delle semplificazioni. Proviamo a ridurre la radice di 32 e la radice di 200 così da scriverle in un’altra forma.
- √32
Iniziamo scomponendo 32=2×2×2×2×2 → 32=24×2.
A questo punto ricomponiamo il radicale → √32 = √24 × √2
Semplificando otteniamo √24 × √2 = 22× √2 =4√2
- √200
Anche in questo caso scomponiamo prima il numero: 200 = 100×2 = 102 ×2 = 52 × 22 × 2
Ri-applichiamo il radicale per ottenere: √200 = √52 × √22 × √2
Semplificando otteniamo: √52 × √22 × √2 = 5×2×√2 = 10√2
La nostra traccia è diventata quindi:
√32+√200 = 4√2 + 10√2
In questo caso la somma può essere eseguita perché c’è una radice comune. Il risultato finale è quindi:
= 14√2.
Esercizio 5
Esprimere le seguenti potenze utilizzando i radicali. Eseguire poi, se possibile, le opportune semplificazioni.
42/3 251/2 34/5
Svolgimento
Ti ricordi le proprietà delle potenze? Quando hai un esponente con una frazione, il numeratore resta come esponente della potenza, mentre il denominatore diventa indice di radice. In base a questa proprietà, possiamo risolvere facilmente gli esercizi sui radicali della traccia.
- 42/3 = 3√42
Ovviamente possiamo scrivere anche il 4 come una potenza (cioè 2 alla seconda).
3√(22)2 = 3√(24) = 3√(23×2) =
= 3√23 × 3√2 = 2 × 3√2.
- 251/2 = √25 = 5.
- 34/5 = 5√34.
In questo ultimo esercizio non è possibile fare alcuna semplificazione. Per cui si arriva direttamente al risultato finale.
Esercizio 6
Semplifica il seguente radicale
6√3/√2
Svolgimento
Ti ricordi come si risolvono gli esercizi con i radicali al denominatore? E’ necessario fare un’operazione che abbiamo chiamato razionalizzazione della radice. Si moltiplica e si divide per la radice presente al denominatore. Eseguiamo i calcoli…
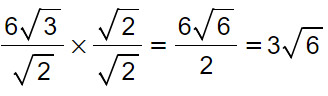
Esercizio 7
Semplifica il seguente radicale
3/(2+√2)
Svolgimento
A differenza del precedente esercizio, il radicale al denominatore compare con una somma. Si ricorre quindi al secondo metodo della razionalizzazione. Si moltiplica e divide per il denominatore cambiando il segno tra i due numeri. In questo modo si sfrutta la regola della somma per la differenza.
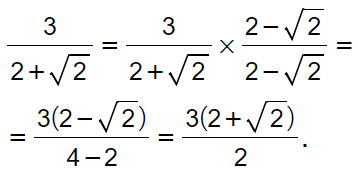
Bibliografia e conclusioni
Gli esercizi sui radicali che abbiamo risolto assieme in questa esercitazione, sono stati assegnati alla George Brown University, l’Università di Toronto in Canada. Se questa lezione ti è stata d’aiuto o se hai un esercizio che vuoi proporre o dei dubbi da chiarire, lascia un commento qui in basso. Ci aiuterà a migliorare la qualità dei contenuti e a fornirti esercitazioni sempre più precise e attente alle vostre richieste.