Il triangolo rettangolo è un triangolo avente un angolo retto, cioè pari a 90°. I lati che si intersecano perpendicolarmente si chiamano cateti, mentre il lato opposto all’angolo retto si chiama ipotenusa.
In questa lezione vedremo tutto quello che c’è da sapere sull’argomento, partendo da uno schema riepilogativo delle formule di un triangolo rettangolo fino ad analizzarne caratteristiche e proprietà. Vedremo, inoltre, che esistono anche alcune figure geometriche particolari, come il triangolo rettangolo isoscele o quello con gli angoli di 30°- 60°- 90°.
Gli appunti che leggerai sono indicati per gli studenti di scuole medie e superiori che devono risolvere problemi di geometria piana. Non rientrano in questa lezione i teoremi sui triangoli rettangoli nella trigonometria, a cui abbiamo dedicato un capitolo a parte visto che fanno parte di un programma differente.
Triangoli rettangoli – prime definizioni
Sui libri di testo e sui vari manuali di geometria si trovano tante definizioni simili il cui significato però è identico. Il triangolo rettangolo è un triangolo avente un angolo retto. Non importa la posizione: l’angolo di 90° può essere alla base o anche al vertice, come puoi vedere nelle figure seguenti.
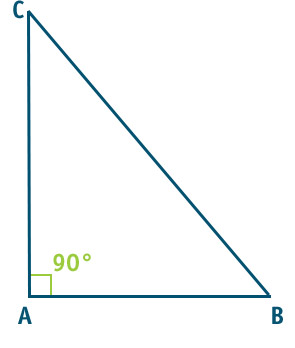
In questa prima figura vedi un triangolo rettangolo con angolo retto alla base nel vertice A. L’angolo di 90° viene in genere indicato con un quadratino, così da poter omettere l’indicazione “90°” essendo poi sottintesa. Hai mai sentito parlare poi di ipotenusa e cateti? Ecco cosa sono:
Cateto triangolo rettangolo: sono i due segmenti che si trovano a ridosso dell’angolo retto. In base alle loro dimensioni, vengono anche detti: cateto minore e cateto maggiore.
Ipotenusa definizione: è il segmento opposto (cioè che si trova esattamente di fronte) all’angolo di 90°.
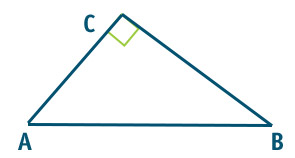
Nella seconda figura abbiamo invece indicato un triangolo rettangolo con angolo retto nel vertice superiore. Mentre alle scuole elementari si preferisce disegnare la figura geometrica nel primo modo, dalle medie in poi si preferisce sempre di più disegnare il triangolo nella seconda maniera.
Nota: su alcuni libri di testo, trovi anche la dicitura “angolo rettangolo” per indicare l’angolo di 90°. Meglio evitare questo tipo di nomi impropri.
Formule triangolo rettangolo
Di seguito andremo ad indicare non solo le formule ma anche le formule inverse dei triangoli rettangoli. Dato quindi il triangolo in figura:
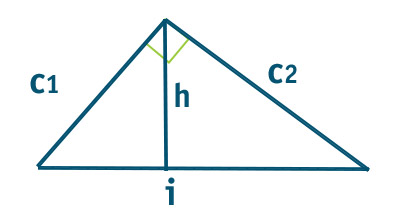
c1 è il cateto minore, c2 è il cateto maggiore, i è l’ipotenusa, h è l’altezza relativa all’ipotenusa, A è l’area e p il perimetro. p1 e p2 sono le proiezioni dei cateti c1 e c2 rispettivamente sull’ipotenusa.
Approfondimenti: tutte le formule dei triangoli
Di seguito abbiamo creato una tabella completa con tutte le formule. Di queste dovrai imparare solo quelle in grassetto. Le altre sono semplicemente delle formule inverse per cui è meglio se le ricavi quando ti serviranno piuttosto che ricordarle a memoria. Puoi trovare tutte le formule (e quelle inverse) anche nel nostro formulario sul triangolo rettangolo.
Tabella con formulario completo
| Perimetro triangolo rettangolo | p=c1+c2+i |
| Formule inverse | |
| Ipotenusa (dal perimetro) | i=p-c1-c2 |
| Cateto (dal perimetro) | c1=p-i-c2 |
| Area triangolo rettangolo (noti i cateti) |
A=(c1×c2)/2 |
| Formule inverse | |
| Cateto (dal’area) | c1=2A/c2 |
| Area triangolo rettangolo (note ipotenusa e altezza) |
A=(i×h)/2 |
| Formule inverse | |
| Ipotesi (dal’area) | i=2A/h |
| Altezza (dal’area) | h=2A/i |
| Teorema di Pitagora | i=√(c1²+c2²) |
| Formule inverse | |
| Cateto 1 (da Pitagora) | c1=√(i²-c2²) |
| Cateto 2 (da Pitagora) | c2=√(i²-c1²) |
| Primo teorema di Euclide | c1²=i×p1 |
| Formule inverse | |
| Ipotenusa (da Euclide) | i=c1²/p1 |
| Proiezione del cateto | p1=c1²/i |
| Secondo teorema di Euclide | h²=p1×p2 |
| Formule inverse | |
| Proiezione del cateto 1 | p1=h²/p2 |
| Proiezione del cateto | p2=h²/p1 |
Approfondimento: formula ipotenusa triangolo rettangolo
Proprietà del triangolo rettangolo
- Uno degli angoli è pari a 90°.
- Gli altri due angoli sono necessariamente acuti, cioè minori di 90° e sono tra loro complementari. La loro somma cioè è pari a un angolo retto.
- Il lato opposto all’angolo retto si chiama ipotenusa. Gli altri si chiamano cateto maggiore e cateto minore.
- L’ortocentro del triangolo rettangolo coincide dove c’è l’angolo retto.
- Un triangolo rettangolo può essere sempre inscritto in una semicirconferenza, di cui l’ipotenusa è il diametro.
- Per il triangolo rettangolo vale il Teorema di Pitagora.
- Valgono inoltre i due Teoremi di Euclide.
Triangoli rettangoli particolari
Triangolo rettangolo isoscele (45-45-90)
In questo lato gli angoli acuti valgono entrambi 45°. Per questa ragione i due cateti sono uguali e si ha una netta semplificazione delle formule. Questa figura la si ottiene tracciando la diagonale del quadrato. Per approfondimenti ti rimandiamo alla lezione di approfondimento sul triangolo rettangolo isoscele.
Triangolo rettangolo 30-60-90
Di fronte il cateto minore c’è l’angolo di 30°, di fronte il cateto maggiore c’è l’angolo di 60°. Grazie a questa caratteristica, il cateto maggiore è pari a metà ipotenusa. In questo modo tutte le formule diventano più semplici e si riducono.
Conclusioni
I triangoli rettangoli sono tra le figure geometriche più presenti non solo nel programma di geometria euclidea. Sarà infatti il punto di partenza per tutto il programma di trigonometria, ma questo è un argomento che affronteremo più avanti.
Se la lezione di oggi ti è stata utile o se l’hai trovata chiara, lascia un commento in basso. Un tuo feedback positivo ci aiuta a migliorare ogni giorno la qualità delle nostre lezioni.
Lezioni chiare e semplici, grazie