L’area del parallelogramma si calcola con la stessa formula del rettangolo, cioè base per altezza. Tuttavia si può determinare la superficie di questa figura anche conoscendo uno dei lati obliqui e l’altezza ad esso relativo oppure, sfruttando le formule trigonometriche, possono essere usati la base e il lato obliquo.
In questa lezione vediamo come calcolare l’area del parallelogramma, fornendo degli appunti utili sia agli studenti delle scuole medie che a quelli delle superiori che hanno già studiato seno e coseno. Iniziamo subito dalle formule più semplici.
Area parallelogramma formula
A=b×h
Per calcolare l’area del parallelogramma è sufficiente moltiplicare la base per l’altezza relativa alla base. Come abbiamo già detto la formula di calcolo è la stessa di quella del rettangolo.La ragione puoi vederla tu stesso in figura.
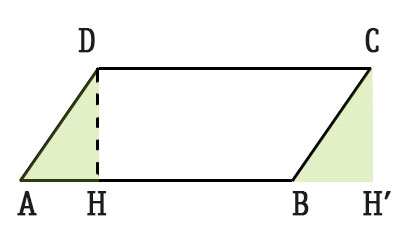
Dato il parallelogramma ABCD, tracciando l’altezza H relativa alla base AB, si ottiene il triangolo evidenziato in verde a sinistra (AHD). Se proviamo a ritagliare questo pezzo ed incollarlo sul lato obliquo BC, si ottiene il rettangolo DHH’C, la cui area si calcola base per altezza. E’ per questa la ragione per cui area del parallelogrammo e quella del rettangolo sono uguali.
In linea teorica è possibile calcolare la superficie di questo quadrilatero anche avendo a disposizione lato obliquo e altezza ad esso relativa. Però quest’ultima informazione è rarissima che si trovi nei problemi di geometria. Per cui generalmente è sufficiente ricordare che l’area è pari alla base per l’altezza.
Calcolare l’area del parallelogramma dato l’angolo
Per gli studenti delle scuole superiori che hanno già studiato trigonometria, esiste un’altra formula
A=b×l×senα
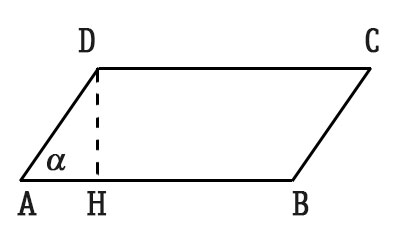
Per calcolare l’area del parallelogramma è possibile moltiplicare la base per il lato obliquo, per il seno dell’angolo compreso.
Dimostrazione
Partiamo dalla formula generale per calcolare l’area, cioè base per altezza.
A=b×h
La base è il lato AB, mentre l’altezza è il segmento DH. Quest’ultimo può essere calcolato sfruttando i teoremi sui triangoli rettangoli della trigonometria. In particolare, considerando il triangolo AHD, si può dire che il cateto DH è uguale all’ipotenusa AD per il seno dell’angolo opposto al cateto, cioè l’angolo α.
Per cui, poiché DH=AD×senα, allora:
A=AB×AD×senα
A=b×l×senα
Come calcolare l’area usando il perimetro
Tornando a formule più semplici, è possibile trovare l’area del parallelogramma in diversi modi, oltre ad usare le due formule viste sopra. Se per esempio la traccia ci fornisce la misura di un perimetro e un’indicazione che ci permetta di relazionare base e altezza, possiamo usare la formula inversa del perimetro per ricavarci la misura di base e altezza. Poi a quel punto sarà semplice applicare la formula dell’area del parallelogramma.
Esercizio
Calcolare l’area di un parallelogramma che ha la base pari a 20 cm e la cui altezza è 2/5 della base. (per la figura fai riferimento all’immagine dell’esercizio 1)
DATI
AB = 20 cm
DH=2/5 × AB
DH=20×2/5
DH = 8 cm
A=(AB×DH)/2=(8×20):2
A = 80 cm²
Conclusioni
Come hai potuto modo di vedere, nella maggior parte dei problemi di geometria che dovrai risolvere, utilizzerai la prima formula vista, che è anche la più facile. Per determinare l’area del parallelogramma sarà infatti quasi sempre sufficiente moltiplicare base per altezza. La parte più difficile sarà, eventualmente, solo il calcolo di queste ultime due.
Se questa lezione ti è stata utile o se hai ancora perplessità o dubbi, lascia un commento nei post in basso. Il nostro staff è a tua disposizione e ti risponderà nel minore tempo possibile.