Riassumiamo in questa pagina tutte le principali formule sulla circonferenza, da quelle utilizzate nella geometria piana e che si studiano anche alle scuole medie, sino a quelle più avanzate di geometria analitica per gli studenti delle scuole superiori.
Nella figura che segue ti abbiamo disegnato una circonferenza: le formule e le lettere saranno tutte riferite a questa prima immagine.
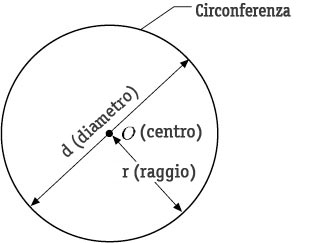
Circonferenza formule geometria piana
Le formule che seguono sono quelle base per calcolare la circonferenza, l’area del cerchio, la misura del raggio o del diametro. Vengono studiate già nelle scuole inferiori.
Calcolo della circonferenza dato il raggio (o il diametro)
C=2πr
C=πd
Formule inverse per trovare raggio o diametro
r=C/2π
d=C/π
Calcolo area del cerchio
A=πr²
A=πd²/4
Formule inverse per trovare raggio o diametro
r=√(A/π)
d=√(4A/π)
Circonferenza formule – geometria analitica
Abbiamo già visto qual è e come si ricava l’equazione della circonferenza generica nella forma canonica. La ripetiamo in questa lezione riepilogativa:
x²+y²+ax+by+c=0
Formula per calcolare la circonferenza noto il raggio e centro
(x-α)²+(y-β)²=r²
dove alfa e beta sono le coordinate cartesiane del centro C(α;β). Attenzione a non confondere queste due coordinate con a,b e c che sono invece i tre coefficienti della circonferenza espressa nella forma canonica.
Da questa equazione è facile calcolare la formula della circonferenza con centro nell’origine.
x²+y²=r²
Da notare che quando il raggio è 1, cioè quando si parla di raggio unitario, si ha quella che viene chiamata circonferenza goniometrica.
Formula raggio circonferenza
In questa lezione riepilogativa ti mostriamo solo le formule sulla circonferenza e non le dimostrazioni, a cui rimandiamo con lezioni di approfondimento. Per calcolare la misura del raggio:
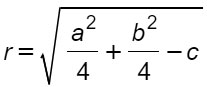
Formula per il calcolo del centro
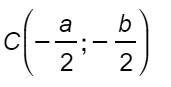
Tutte quelle che abbiamo visto fino ad ora sono le formule della circonferenza che si trovano generalmente su tutti i libri di testo. Quelle che ti mostriamo di seguito sono invece delle formule che si ricavano dall’esperienza e che possono essere utilizzate in tantissimi problemi di geometria analitica.
Formula per calcolare il raggio noto il centro e un punto della circonferenza
In questo caso semplicemente si sfrutta la definizione di circonferenza: è il luogo geometrico dei punti equidistanti dal centro. Poiché quindi il raggio si tiene costante, semplicemente basta calcolare la distanza tra due punti.
Dato il centro C(α;β) e un punto della circonferenza P(xP,yP), il raggio si calcola con la formula:
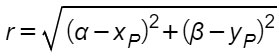
Formula della circonferenza per 3 punti
In questo caso si impone l’appartenenza di ogni singolo punto alla circonferenza. Come? Si sostituiscono le sue coordinate al posto della x e della y nella formula della circonferenza. Visto che sono 3 punti, ci saranno 3 equazioni in 3 incognite (a, b e c). Si ottiene quindi un sistema di equazioni di primo grado.
Dati quindi tre punti generici P1(xP1;yP1), P2(xP2;yP2) e P3(xP3;yP3), il sistema che si va a costruire è:
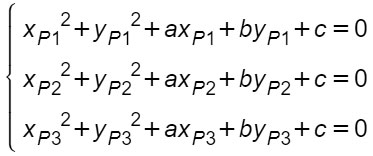
Conclusioni
Nello svolgimento degli esercizi, ti renderai conto che non sempre la circonferenza ha formule precise da usare, ma spesso si tratta di metodi di calcolo. E’ il caso ad esempio degli esercizi sulle tangenti alla circonferenza. Abbiamo dedicato ben due lezioni di approfondimento sull’argomento che ti consigliamo di leggere:
- Retta tangente alla circonferenza passante per un punto dato
- Formula di sdoppiamento per trovare la tangente ad una figura
Se questa lezione ti è stata utile, se hai ancora dei dubbi o delle perplessità, o hai bisogno di integrare ulteriori formule, lascia un commento in basso. Il nostro staff è a tua disposizione e ci aiuterai a migliorare la qualità delle lezioni.