Il baricentro del triangolo è il punto di intersezione delle tre mediane. Per poterlo disegnare è sufficiente disegnare la mediana relativa ad ogni lato e il loro punto in comune viene chiamato baricentro.
In questa lezione vedremo non solo la definizione di questo punto caratteristiche ma analizzeremo anche come cambia questo a seconda dei tipi di triangoli. Per gli studenti di geometria analitica vedremo anche formule e un semplice esercizio sul calcolo del baricentro.
Che cos’è il baricentro di un triangolo
Ne abbiamo già dato una definizione: è il punto di intersezione delle mediane del triangolo. Ti ricordi che cos’è la mediana? E’ il segmento che congiunge un vertice con il punto medio del lato opposto. Proviamo quini a disegnare il baricentro di un triangolo scaleno acutangolo.
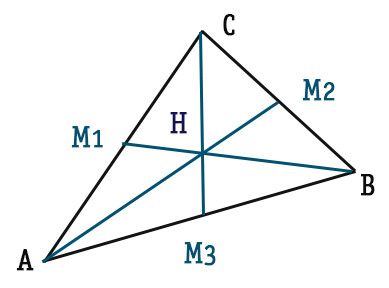
Dato il generico triangolo ABC, abbiamo disegnato le mediane relative ad ogni lato. Dalla loro intersezione si ottiene il punto H, baricentro del triangolo.
Caratteristiche e proprietà del baricentro
Ti ricordi che l’ortocentro e il circocentro potevano essere anche esterni alla figura? Per il baricentro dei triangoli, ciò non può accadere per cui la prima proprietà di questo punto è:
- il baricentro del triangolo è un punto sempre compreso nel perimetro della figura;
- il baricentro divide ogni mediana in due parti. Quella che contiene il vertice è il doppio dell’altra.
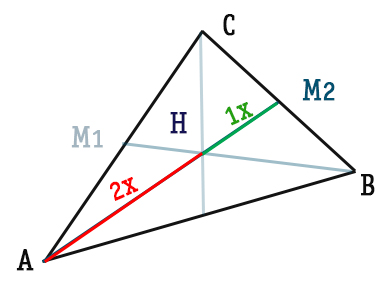
In base alla proprietà appena vista, possiamo dire che AH=2HM2.
- il baricentro di un triangolo equilatero coincide con l’ortocentro e con il circocentro.
Il baricentro del triangolo in geometria analitica
Questa seconda parte della lezione è dedicata agli studenti delle scuole superiori che stanno studiando geometria analitica. Esiste una formula che, dati i vertici del triangolo, permette di calcolare il baricentro in pochi semplici passaggi.
Formula baricentro
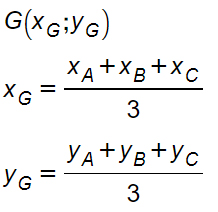
dove A, B e C sono i tre vertici del triangolo di cui sono note le coordinate cartesiane.
Per calcolare le coordinate del baricentro del triangolo bisogna quindi:
- fare la media aritmetica delle ascisse dei tre vertici. Cioè si sommano le tre x e si fa il risultato diviso 3. In questo modo si ottiene l’ascissa del baricentro.
- fare la media aritmetica delle ordinate dei tre vertici. Cioè si sommano le tre y e si fa il risultato diviso 3. In questo modo si ottiene invece l’ordinata del baricentro.
Esempi ed esercizi svolti
Esercizio 1
Dato il triangolo di vertici A(6;0) B(2;2) e C(7;7), calcolare le coordinate del baricentro G.
Applichiamo subito la formula appena vista. Possiamo così scrivere che:
xG=(6+2+7)/3=15/3=5
yG=(0+2+7)/3=9/3=3
G(5;3)
Esercizio 2
Dato il triangolo con baricentro G(5;3) e noti due vertici A(6;0) e B(2;2), determinare il terzo vertice C.
Si tratta dello stesso esercizio visto prima ma questa volta bisogna fare il procedimento al contrario. Cioè dovremo usare la formula inversa del baricentro per trovare uno dei vertici. Riscriviamo così la formula come l’abbiamo vista prima, esplicitando tutti i dati forniti dalla traccia e lasciando le coordinate di C come incognita.
xG=(xA+xB+xC)/3 → 5=(6+2+x)/3 → 15=6+2+x → x=15-6-2
xC=7
yG=(yA+yB+yC)/3 → 3=(0+2+y)/3 → 9=2+y
yC=7
C(7;7).
Conclusioni
Il calcolo del baricentro di un triangolo in geometria analitica è una delle operazioni più semplici di tutto il programma. Proprio per questo troverai ben pochi esercizi che te lo richiederanno. Tuttavia è utile da sapere e da ricordare qualora dovesse servire.
Se questa lezione ti è stata d’aiuto o se hai bisogno di ulteriori chiarimenti, lascia un commento in basso. Il nostro staff ti risponderà nel minor tempo possibile.