Le disequazioni goniometriche sono delle disequazioni nelle quali la variabile x compare anche come argomento di una o più funzioni goniometriche.
Per risolvere le disequazioni goniometriche è necessario calcolare tutti gli angoli che la soddisfano. Ne esistono di diversi tipi: dalle parametriche alle lineari. In questa pagina vedremo come si risolvono le disequazioni goniometriche fondamentali con alcuni riferimento ad esempi ed esercizi più complessi.
Disequazioni goniometriche elementari
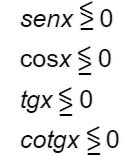
Quelle che hai appena visto sono la forma base più semplice che possa essere trovata negli esercizi. L’obiettivo è sempre ricondursi ad una di queste quattro diseguaglianze elementari. Per ciascuna di queste ci sarà un risultato differente. Vediamo singolarmente i casi appena presentati.
Caso 1
![]()
Immaginiamo di avere la disequazione goniometrica elementare senx>m. Per quanto detto nello studio della funzione seno, quest’ultima esiste solo per valori compresi tra -1 e +1. Questo vuole dire che, per senx>m:
- se m<-1, la disequazione è sempre verificata, cioè è valida ∀x∈R.
- se m>+1, la disequazione è impossibile.
- se -1<m<+1, analizziamo il grafico in figura:
Le soluzioni sono date dagli intervalli dei valori dell’arco x per i quali il grafico della funzione si trova sopra il grafico della sinusoide:
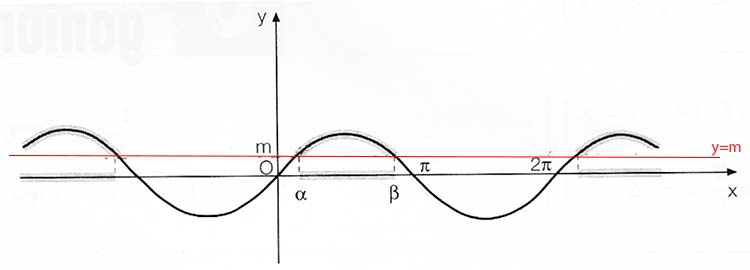
Le soluzioni delle disequazioni trigonometriche elementari con il seno sono date dagli intervalli dei valori dell’angolo x per i quali il grafico della sinusoide si trova sopra la retta y=m. Considerando solo l’intervallo che va da 0 a 2π, gli angoli per i quali senx=m sono in figura α e β. Possiamo quindi scrivere le soluzioni della disequazione nel seguente modo:
α+2kπ < x < β+2kπ
Si procede in modo del tutto analogo nel caso si debba risolvere la disequazione goniometrica elementare senx<m (oppure senx≤m). Ricordiamo soltanto che, in questo caso, se m<-1 la disequazione è impossibile. Se m>1 la disequazione è verificata sempre cioè ∀x∈R.
Esempio
Risolviamo la disequazione goniometrica 2senx-1≤0
Abbiamo senx≤1/2
Rappresentiamo graficamente la situazione:
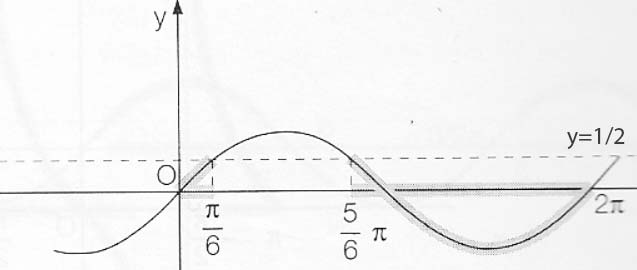
Analizzando il grafico si può dedurre che la disequazione goniometriche è verificata per
2kπ < x <π/6+2kπ ∪ 5/6π+2kπ < x <2π+2kπ
Caso 2
![]()
Immaginiamo di avere cosx>n.
- Se n<-1, la disequazione è verificata sempre, cioè ∀x∈R.
- Se n>1, la disequazione è impossibile.
- Se -1≤n≤+1, analizziamo il grafico della cosinusoide.
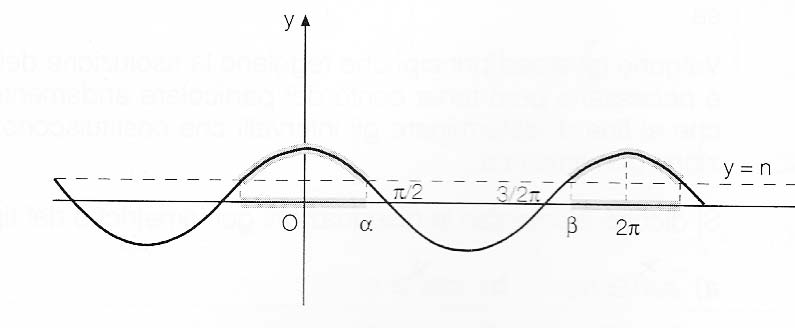
Le soluzioni della disequazione goniometrica sono date dagli intervalli dei valori di x per i quali il grafico della funzione y=cosx si trova sopra il grafico della retta y=n. In tali intervalli è infatti verificata la disuguaglianza cosx>n. Chiamati α e β gli angoli, compresi tra 0 e 2π, per i quali il coseno ha valore n, possiamo scrivere le soluzioni della disequazione nel seguente modo:
2kπ ≤ x≤α+2kπ ∪ β+2kπ<x<2π+2kπ
In modo del tutto analogo si procede per la risoluzione dell’equazione goniometrica elementare cosx<n (oppure cosx≤n); in questo caso, se n<-1 la disequazione è impossibile. Se n>1 la disequazione è verificata ∀x∈R.
Esempio
Risolviamo la disequazione trigonometrica 2cosx+√2≥0
Iniziamo sistemandoci tutti i termini al posto giusto:
cosx≥-√2/2
Rappresentiamo graficamente la funzione coseno e la retta orizzontale y=-√2/2.
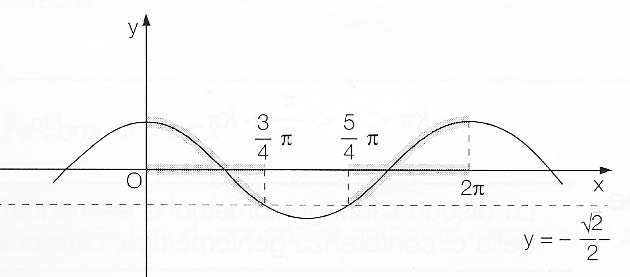
I valori che soddisfano la disequazione goniometrica sono tutti quelli che stanno al di sopra la retta orizzontale disegnata. Per cui possiamo dire che la soluzione dell’esercizio è:
2kπ < x <3/4π+2kπ ∪ 5/4π+2kπ < x <2π+2kπ
Caso 3
![]()
Analogamente a quanto fatto con i primi due casi, analizziamo tgx>p. Si tracci il grafico della tangente:
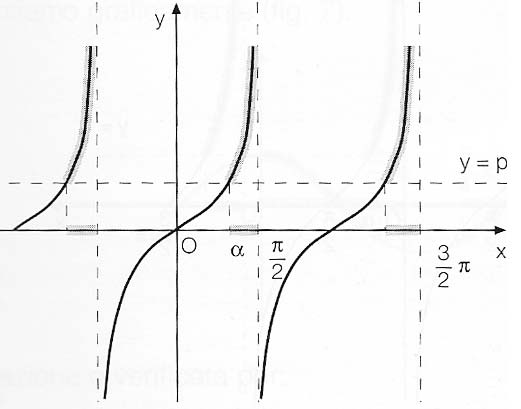
Detto α (con 0<α<π, α≠π/2) l’arco per il quale la tangente ha valore p, possiamo scrivere le soluzioni della disequazione goniometrica come segue:
kπ+α< x<π/2+kπ
Dovendo risolvere la disequazione tgx>p con p<0, si dovrà tenere presente che l’angolo α (compreso tra 0 e 180°) per il quale la tangente ha valore p, è maggiore di π/2. Le soluzioni si scriveranno come segue:
kπ+α≤x<π/2+kπ ∪ α+kπ<x<π+kπ
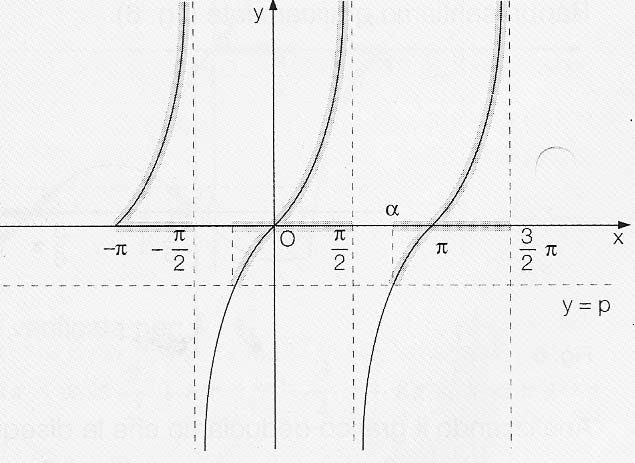
Considerazioni analoghe valgono per la risoluzione delle disequazioni goniometriche elementari con tgx<p (o con il simbolo minore e uguale).
Esempio
Risolviamo la disequazione trigonometrica 3tg²x-2√3tgx+1>0
Si tratta di un polinomio che può essere ridotto a quadrato di binomio. Per cui si ottiene:
(√3tgx-1)²>0
Essendo un quadrato sempre positivo o al limite nullo, la disequazione è soddisfatta per i seguenti valori di tgx.
tgx≠+√3/3
ossia dai seguenti valori dell’angolo x:
x≠π/6+kπ ∪ x≠π/2+kπ
Caso 4
![]()
Come nei casi precedenti, sia cotgx>q. Analizziamo il grafico in figura:
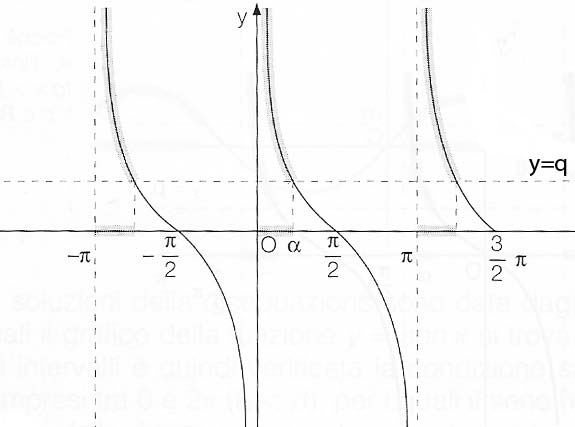
Poiché il codominio della funzione y=cotgx è l’insieme R dei numeri reali, la disequazione cotgx>q è sempre risolvibile.
Detto α l’angolo per il quale la cotangente ha valore q (0<α<π), possiamo scrivere le soluzioni della disequazione goniometrica nel seguente modo:
kπ< x<α+kπ
Considerazioni analoghe valgono per la risoluzione della disequazione cotgx<q (e con il segno minore e uguale).
Esempio
Risolviamo la disequazione trigonometrica cotgx>√3
Rappresentiamo graficamente la traccia dell’esercizio:
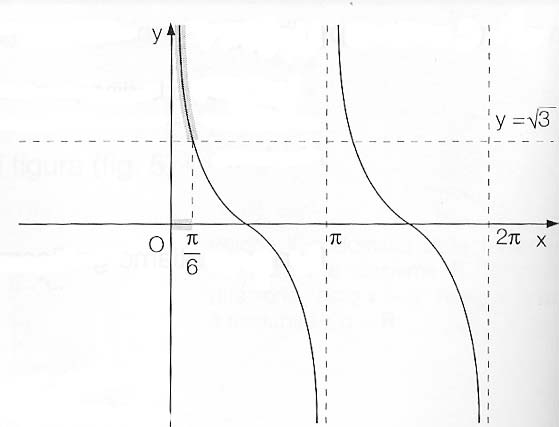
La disequazione è verificata per
kπ<x<π/6+kπ
Un metodo di risoluzione alternativo
Le disequazioni goniometriche elementari possono essere anche risolte con l’ausilio della circonferenza goniometrica, oltre che con il metodo appena presentato. Ad esempio, la disequazione senx≤1/2 che abbiamo trattato nel primo esempio, può essere risolta facendo riferimento alla figura seguente.
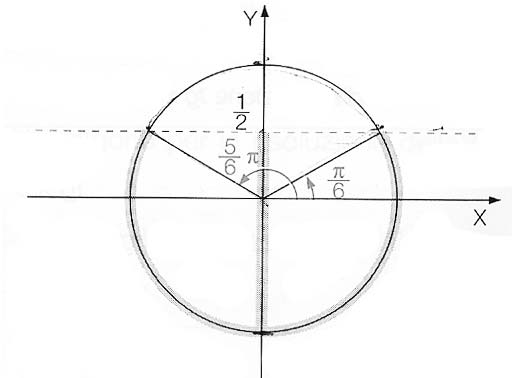
Si inizia prendono quei valori degli angoli per cui il seno vale 1/2. Cioè l’angolo π/6 e 5/6π. Sopra la linea tratteggiata ci sono tutti gli angoli che hanno un seno superiore a 1/2. Sotto la linea tratteggiata ci sono tutti quegli angoli che rispettano la disequazione trigonometrica senx<1/2. Per cui si ottengono le soluzioni:
2kπ < x <π/6+2kπ ∪ 5/6π+2kπ < x <2π+2kπ
Conclusioni
Abbiamo visto come risolvere le disequazioni goniometriche elementari in due diversi metodi. La scelta dell’uno o dell’altro è soggettiva e, come dimostrato, non cambia il risultato ottenuto. Anche negli esercizi più complessi sarà necessario ricondursi ad una di queste 4 forme base.
In caso di dubbi o perplessità o se la lezione è stata di tuo aiuto, lascia un commento positivo in basso. Ci aiuterà a crescere e a regalarti ogni giorno tante lezioni gratuite di matematica.