Come si fa a portare fuori radice un numero? C’è differenza tra una radice quadrata e una radice cubica in questo calcolo? E’ possibile avere qualche esempio ed esercizio svolto? Grazie – Simona
SOLUZIONE
Per portare un numero fuori dalla radice consente di semplificare notevolmente gli esercizi con i radicali. Il metodo di calcolo per trasportare un fattore fuori al segno di radice è piuttosto semplice.
Sui libri di testo di matematica viene in genere illustrato un modo per portare fuori radice un numero che comporta la suddivisione del radicale in vari prodotti di radicali. Il nostro metodo, invece, è universale e molto più semplice. Vediamo subito come procedere con un esempio pratico.
Come portare fuori dalla radice quadrata
Esercizio 1
Semplificare il numero √96 portando fuori dalla radice i fattori opportuni
- Il primo passo consiste nel riscriverci il numero 96 in fattori primi. Così come si faceva nel calcolo del mcm ci scriviamo quelli che sono i numeri primi che, moltiplicati tra loro, ci danno come risultato 96.
 Costruiamo una piccola tabella dove segniamo il numero 96. Sulla destra mettiamo il primo numero che ci viene in mente per cui 96 è divisibile, ad esempio 2. Facciamo 96 diviso 2 e il risultato lo riportiamo sotto. 48 a sua volta è divisibile per 2 (che scriviamo a destra) e il risultato lo riportiamo a sinistra sotto. Continuiamo così fino a quando non arriviamo al numero 1.
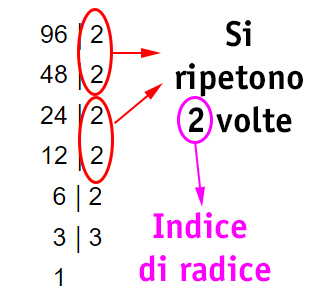
Costruiamo una piccola tabella dove segniamo il numero 96. Sulla destra mettiamo il primo numero che ci viene in mente per cui 96 è divisibile, ad esempio 2. Facciamo 96 diviso 2 e il risultato lo riportiamo sotto. 48 a sua volta è divisibile per 2 (che scriviamo a destra) e il risultato lo riportiamo a sinistra sotto. Continuiamo così fino a quando non arriviamo al numero 1. - A questo punto, essendoci una radice quadrata (cioè indice 2), cerchiamo tutti i gruppi di numeri che si ripetono 2 volte.
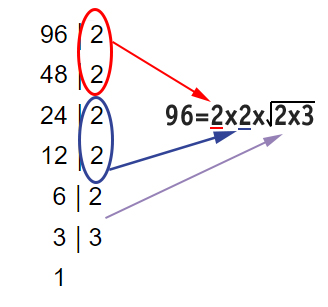
- Riscriviamo il numero da portare fuori radice come la moltiplicazione dei numeri cerchiati (presi una sola volta per gruppo) per la radice dei numeri non cerchiati.

- Quindi possiamo scrivere:√96 = 2×2×√(2×3) = 4√6
Verifica del risultato
Per verificare la correttezza del procedimento, prova ad elevare al quadrato il numero appena ottenuto (cioè 4√6). Se ottieni il numero di partenza, allora il risultato si trova. Nel nostro esercizio:
(4√6)²=16×6=96 → Risultato corretto
Come portare un numero fuori dalla radice cubica
Il procedimento è perfettamente analogo al precedente, c’è un’unica sostanziale differenza. In questo caso andremo a cerchiare i gruppi di 3 numeri uguali visto che l’indice di radice è pari a 3. Proviamo a risolvere lo stesso esempio precedente stavolta provando a portare il numero fuori da radice terza.
Esercizio 2
Semplificare il numero ³√96 portando fuori dalla radice i fattori opportuni.
Anche in questo caso iniziamo a compilare una tabella con la scomposizione del numero di partenza in fattori primi. A questo punto formiamo dei gruppi da 3 di numeri uguali.
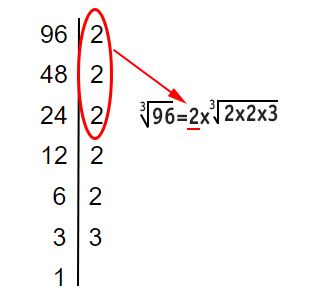
A questo punto possiamo scrivere il risultato seguendo la solita regola:
- si prende un numero per ogni gruppo
- il numero del gruppo va fuori radice
- tutti gli altri all’interno con il segno “per”.
Possiamo quindi dire che:
³√96=2׳√(2×2×3)=2³√12
Verifica del risultato
In questo caso basta elevare al cubo il risultato ottenuto e verificare che il risultato coincida con il numero di partenza.
(2³√12)³=8×12=96.
Il metodo classico
E’ quello che viene insegnato a scuola e si bassa sulle proprietà dei radicali. Bisogna prendere il numero da portare fuori radice e lo si scompone in fattori primi.
Esercizio 3
Semplificare il numero √96 portando fuori dalla radice i fattori opportuni.
E’ l’esercizio numero 1, che stavolta proviamo a risolvere con il metodo classico. Riscriviamo quindi il numero 96 come la moltiplicazione di tanti numeri primi.
√96=√(2×2×2×2×2×3)
√96=√(25×3)
A questo punto scriviamo ogni fattore della moltiplicazione con la radice:
√96 = √25×√3 = (√2²×√2²×√2)×√3 =
Nel passaggio precedente abbiamo riscritto la radice quadrata di 2 elevato a 5 come il prodotto di potenze con la stessa base (vedi proprietà delle potenze).
= 2×2×√2×√3 =
=4×√6
Anche il secondo metodo per portare dei numeri fuori dalle radici è piuttosto semplice, ma forse per gli studenti è un po’ più macchinoso. Per questa ragione noi consigliamo di imparare il primo che è più semplice ed immediato. Tuttavia la scelta è indifferente, visto che portano entrambi i metodo alla stessa soluzione.
Conclusioni
Il metodo che abbiamo illustrato in questa lezione può essere applicato a qualsiasi tipo di radicale. Si può portare fuori dal segno di radice quadrata, cubica, quarta… La cosa importante è ricordarsi di scegliere bene il numero di fattori da inserire in ogni gruppo.
 Costruiamo una piccola tabella dove segniamo il numero 96. Sulla destra mettiamo il primo numero che ci viene in mente per cui 96 è divisibile, ad esempio 2. Facciamo 96 diviso 2 e il risultato lo riportiamo sotto. 48 a sua volta è divisibile per 2 (che scriviamo a destra) e il risultato lo riportiamo a sinistra sotto. Continuiamo così fino a quando non arriviamo al numero 1.
Costruiamo una piccola tabella dove segniamo il numero 96. Sulla destra mettiamo il primo numero che ci viene in mente per cui 96 è divisibile, ad esempio 2. Facciamo 96 diviso 2 e il risultato lo riportiamo sotto. 48 a sua volta è divisibile per 2 (che scriviamo a destra) e il risultato lo riportiamo a sinistra sotto. Continuiamo così fino a quando non arriviamo al numero 1.