Quanto vale il coseno di 30 gradi? Esiste un metodo per arrivare a questo valore, tipo una dimostrazione per calcolare il coseno di 30°? Va bene se lo calcolo con la calcolatrice – Grazie, Chiara.
Risposta
Per gli studenti che si approcciano per la prima volta al programma di trigonomietria, ricordare a memoria i valori di seno e coseno degli angoli noti è sempre un po’ un problema. Chiara ci ha chiesto di risolvere i suoi dubbi riguardo al calcolo del coseno di 30° e in questa lezione vediamo di darle una spiegazione chiara e semplice e alcuni consigli per ricordarne il valore.
Iniziamo subito vedendo quanto vale il coseno di 30 gradi.
Se esprimiamo l’angolo in radianti, possiamo invece scrivere:
cosπ/6=√3/2
Se non ricordi come è stato trasformato l’angolo in radianti, ti consigliamo di dare un’occhiata alla lezione sulla conversione gradi radianti.
Coseno di 30 gradi, dimostrazione
Per ricavare il valore di cos30° in maniera semplice, ti consigliamo di disegnare la circonferenza goniometrica e di staccare un angolo di trenta gradi in senso antiorario dall’asse delle ascisse.
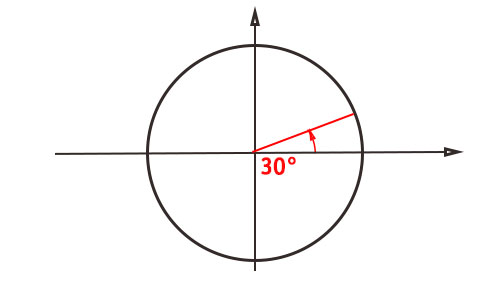
A questo punto, partendo dal raggio disegnato in figura con il colore rosso, disegna la retta verticale e quella orizzontale, che corrispondono rispettivamente al seno e al coseno di 30°.
Approfondimenti: come si disegnano seno e coseno per definizione
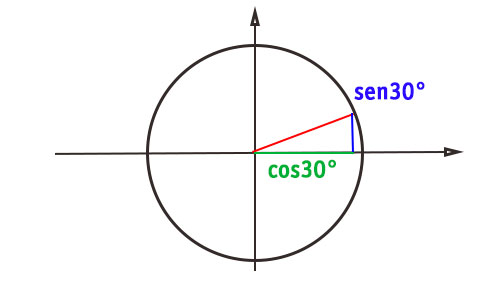
Abbiamo così ottenuto un triangolo rettangolo, dove il coseno di 30 e il seno di 30 sono i cateti maggiore e minore. Il raggio, che nella circonferenza goniometrica vale 1, è invece il segmento disegnato in rosso.
Che tipo di triangolo è? Sicuramente è un triangolo rettangolo particolare perché ha gli angoli di 30°, 90° e 60°.
In questo tipo di triangoli vale che il cateto minore è la metà dell’ipotenusa. Quindi se
Ipotenusa=r=1 → Cateto Minore= sen30°=1/2
Per calcolare il coseno di 30, applichiamo la formula inversa del teorema di Pitagora. Quindi possiamo scrivere che vale:
Ipotenusa²=Cateto²+cateto² → r²=sen30²+cos30²=1
(cos30°)²=1-(sen30°)²
cos30°=√[1-(1/2)²]
cos30°=√(1-3/4)
cos30°=√3/2
Abbiamo quindi dimostrato quanto vale il coseno di 30, semplicemente utilizzando il teorema di Pitagora e pochi semplici passaggi algebrici.
Consigli per gli studenti
E’ vero che all’inizio non è facile imparare a memoria i valori delle funzioni goniometriche. Come si fa a ricordare il coseno di 30°, il seno di 45° e tutti gli altri angoli? Con un po’ di pratica e facendo tanti esercizi.
Il nostro consiglio è di impararli a memoria, perché in questo modo diventerà molto più semplice trovare i valori per angoli più complessi utilizzando poi le regole degli archi associati.
Inoltre anche la calcolatrice scientifica da questo punto di vista non è tanto utile, perché se proviamo a calcolare il coseno di 30 il risultato è 0,866… A noi serve il risultato con il radicale e non quello con la virgola.
L’aspetto positivo però è che i valori da ricordare sono sostanzialmente 2: √3/2 (per il coseno di 30°) e 1/2 (per il seno di 30°). Per l’angolo di 60°, ad esempio, i valori sono semplicemente invertiti, cioè cos60°=1/2 e sen60°=√3/2. Quindi alla fine dei conti dovrai ricordare solo questi due numeri!