Le formule parametriche del seno e del coseno vengono utilizzate in trigonometria per esprimere le principali funzioni goniometriche (seno e coseno) in funzione di un parametro t. Diventeranno importanti soprattutto con l’uso degli integrali, per cui è opportuno approfondire l’argomento.
In questa lezione vedremo quali sono le formule parametriche, come si dimostrano e in quali tipi di esercizi di trigonometria vanno utilizzate. Per la dimostrazione è importante ricordare le formule di duplicazione del seno e del coseno, perché si parte proprio da queste ultime.
Formule parametriche tabella
Formule parametriche seno
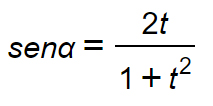
Formule parametriche coseno
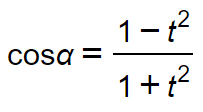
Formule parametriche tangente
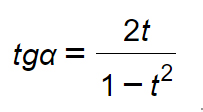
Per entrambe vale che tg(α/2)=t
Le formule che hai appena visto vengono chiamate parametriche perché prevedono al loro interno l’uso di un parametro t. Queste ci permettono di esprimere il seno e il coseno di un arco in funzione razionale della tangente dell’arco metà. Esse sono valide solo per:
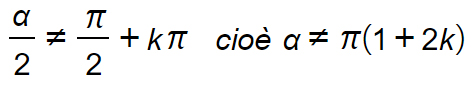
Dimostrazione formule parametriche seno
Non è importa che il tuo professore a scuola le abbia studiate o meno. E’ il caso almeno di leggere la dimostrazione delle formule parametriche perché potrebbero servirti in futuro. Iniziamo subito con il seno partendo dalle formule di duplicazione.
sen2α=2senαcosα
Andiamo a sostituire α/2 al posto di α per ottenere quindi:
sen2α=2sen(α/2)cos(α/2)
e poiché vale sen²α+cos²α=1 → sen²(α/2)+cos²(α/2)=1
possiamo sostituire ancora:
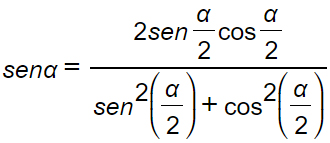
da cui, dividendo numeratore e denominatore per cos²α/2 otteniamo:
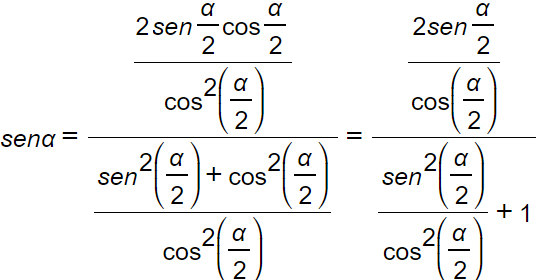
Ricordi la definizione di tangente di un angolo? E’ il seno fratto il coseno. Per cui abbiamo:
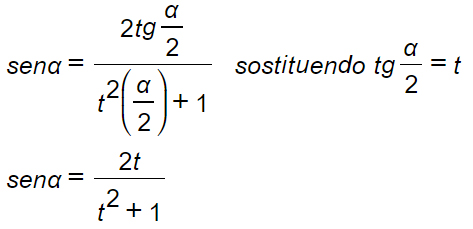
Abbiamo così dimostrato le formule parametriche per il seno.
Dimostrazione formule parametriche coseno
La dimostrazione è del tutto analoga a quella utilizzata per il seno. Quindi si parte da quelle di duplicazione:
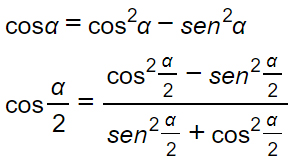
Dividiamo numeratore e denominatore per il coseno al quadrato di α/2. Otteniamo quindi:
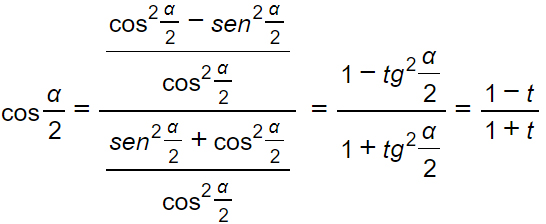
Esercizi sulle formule parametriche
Sei pronto a questo punto per provare qualche esercizio? In questa parte della lezione ci concentriamo ora su qualche esempio svolto e commentato, così da aiutarti con la risoluzione.
Esempio 1
Sapendo che tgα=1/3, determiniamo nel modo più semplice sen2α e cos2α.
Per le formule parametriche si ha:
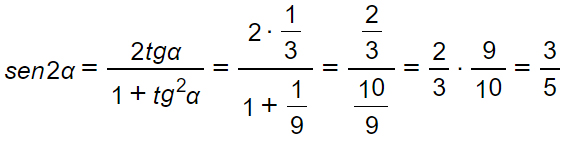
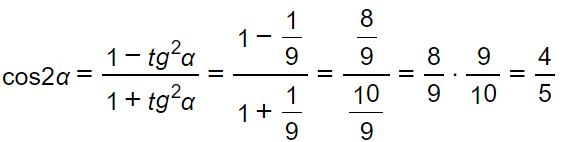
Commento: l’esercizio è piuttosto semplice. Il metodo utilizzato per risolverlo è stato quello di moltiplicare gli angoli per due. Quindi invece di considerare t come la tangente di α/2, abbiamo lasciato l’angolo come α.
Esempio 3
Esprimiamo la seguente espressione come funzione razionale di un’unica variabile.
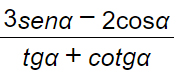
Ponendo tg α/2=t possiamo quindi scrivere:
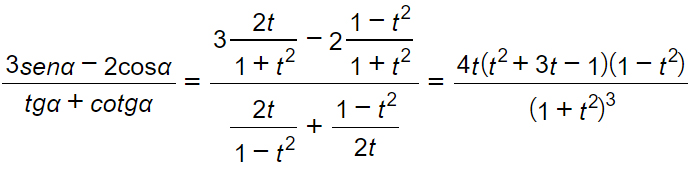
Conclusioni
Si conclude così la lezione sulle formule parametriche. Come hai potuto notare, si tratta di una semplice formula che purtroppo va imparata a memoria ma, fidati, ti servirà soprattutto quando ti ritroverai a risolvere gli integrali. Inoltre non è particolarmente difficile da memorizzare.
Per qualsiasi dubbio o curiosità ti invitiamo a scriverci un messaggio utilizzando la nostra pagina contatti, o lasciando un commento sotto.