Le formule di prostaferesi vengono studiate generalmente poco dopo le formule di addizione e sottrazione nel programma di trigonometria. Vengono infatti utilizzate per riscrivere in maniera diversa e più semplice le addizioni e le sottrazioni tra le seno e coseno. Permettono la risoluzione di esercizi in cui ci sono funzioni goniometriche strane come cos5x, sen3x, ecc… Vediamo subito quali sono le formule di prostaferesi con una tabella completa.
Tabella formula di prostaferesi
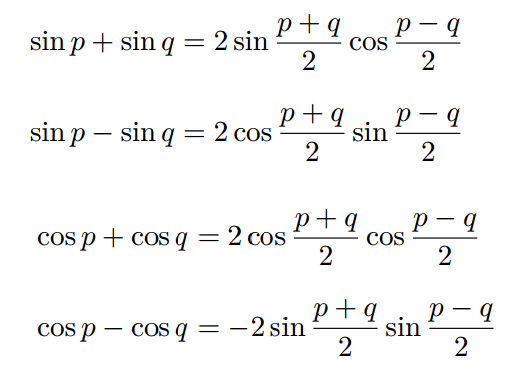
E’ possibile utilizzare le formule di prostaferesi anche per trasformare la somma e la differenza della tangente o della cotangente di due angoli. Infatti possiamo scrivere che:
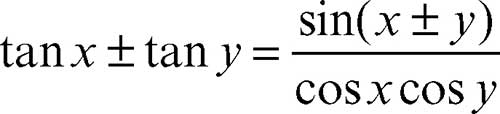
Per ottenere la formula di prostaferesi per la cotangente, basta invertire numeratore e denominatore dell’ultima formula.
Dimostrazione delle formule di prostaferesi
Consideriamo le formule di addizione del seno:
- sen(α+β)=senαcosβ+cosαcosβ
- sen(α-β)=senαcosβ-cosαcosβ
Proviamo a sommare membro a membro le due formule. Si ottiene così:
sen(α+β)+sen(α-β)=senαcosβ+cosαcosβ + senαcosβ-cosαcosβ
Si eliminano i termini opposti ottenendo:
sen(α+β)+sen(α-β)=2senαcosβ
Poniamo:
- α+β=p
- α-β=q
Sommando e sottraendo questi due valori possiamo ottenere:
- sommando: α+β+α-β=p+q → 2α=p+q→α=(p+q)/2
- sottraendo:α+β-α+β=p-q→2β=p-q→β=(p-q)/2
Sostituendo i dati appena ottenuti nell’equazione segnata in arancione, abbiamo:
sen(p)+sen(q)=2sen[(p+q)/2]cos[(p-q)/2]
Abbiamo così dimostrato la formula di prostaferesi per la somma del seno. Per dimostrare la sottrazione del seno, semplicemente si sottraggono membro a membro i termini precedentemente addizionati. In maniera del tutto analoga, te lo lasciamo come esercizio per casa, si possono ottenere le formule di prostaferesi per il coseno andando ad agire sulle formule di addizione e sottrazione del coseno.
Per trasformare anche la somma e la differenza della tangente o della cotangente di due angoli, si dimostra invece che:
tgα±tgβ=senα/cosα±senβ/cosβ
tgα±tgβ=(senαcosβ±cosαsenβ)/cosαcosβ
tgα±tgβ=sen(α+β)/cosαcosβ
Consigli ed applicazioni
CURIOSITA’: sai che significa la parola prostaferesi? Deriva dall’unione di prosthesis e aphairesis due termini di origine greca che significano rispettivamente somma e differenza.
Le formule di prostaferesi servono a trasformare in un prodotto la somma o la differenza di funzioni goniometriche. Vediamo più nel dettaglio come si utilizzano queste formule con alcuni esercizi svolti con difficoltà crescente.
Esempio 1
Trasformiamo in prodotto la somma: √3/2+senα
Dobbiamo quindi utilizzare la formula di prostaferesi della somma del seno:
√3/2+senα=sen60°+senα=2sen[(60+α)/2]/2⋅cos[(60-α)/2]/2
Esempio 2
Trasformiamo in prodotto la somma: sen7x-sen3x
In questo caso utilizziamo la formula di prostaferesi della differenza del seno:
sen7x-sen3x=
=2cos[(7x+3x)/2]/2⋅sen[(7x-3x)/2]/2=
=2cos5x⋅sen2x.
Esempio 3
Trasformiamo in prodotto la somma: cos20°+cos50°+2cos35°
Attenzione: piuttosto che usare le formule di prostaferesi con 3 addendi, risolviamo due somme alla volta.
cos20°+cos50°+2cos35°=
=2cos[(20°+50°)/2]cos[(20°-50°)/2]+2cos35°=
=2cos35°cos15°+2cos35°
A questo punto piuttosto che provare calcoli e passaggi complessi con le formule di prostaferesi, eseguiamo un raccoglimento a fattor comune totale (o messa in evidenza) di 2cos35°
=2cos35°(cos15°+1)
A questo punto, poiché il 1 possiamo scriverlo anche come cos0°, allora abbiamo:
=2cos35°(cos15°+cos0°)=
=2cos35°⋅2cos15°/2⋅cos15°/2=
=4cos35°cos²15°/2.
Esempio 4
Trasformiamo in prodotto la somma: senx+cosy
Non possiamo utilizzare direttamente le formule di prostaferesi dato che non c’è una somma o differenza di seni o di coseni, ma il problema è misto. Trasformiamo quindi il coseno in seno usando gli archi associati. Per cui abbiamo:
senx+cosy=
=sex+sen(90°-x)=
=2sen[(x+90-y)/2]cos[(x-90+y)/2]=
=2sen[(x-y)/2+45°]cos[(x-y)/2-45°]
Da questo ultimo esercizio, come hai potuto notare, è possibile trasformare in un prodotto anche la somma o la differenza di un seno e di un coseno. Per usare infatti le formule viste in tabella ad inizio capitolo, è sufficiente trasformare il coseno nel seno dell’angolo complementare e successivamente applicare le formule di prostaferesi.