Le diagonali del quadrato sono due segmenti che congiungono i vertici opposti della figura. Sono tra loro uguali e perpendicolari. Ci sono diverse formule che riguardano il calcolo della diagonale di un quadrato.
Indice degli argomenti trattati
- Diagonali quadrato – cosa sono?
- Formula diagonale quadrato
- Come calcolare la diagonale di un quadrato?
- Come calcolare il lato di un quadrato conoscendo la diagonale?
- Esempio
- Suggerimenti e consigli
Diagonali quadrato – cosa sono?
La definizione è quella che abbiamo riportato all’introduzione di questa guida. La diagonale di un quadrato è il segmento che congiunge due vertici opporti del quadrato.
Le diagonali del quadrato hanno le seguenti caratteristiche:
- sono congruenti, cioè sono uguali tra loro;
- sono perpendicolari, cioè dalla loro intersezione si formano quattro angoli retti;
- la loro misura è sempre maggiore del lato del quadrato stesso;
- dividono il quadrato in due triangoli rettangoli isosceli congruenti, cioè uguali.
- sono le bisettrici degli angoli interni del quadrato
Formula diagonale quadrato
d=l√2
La diagonale del quadrato si calcola moltiplicando il lato per la radice di 2.
Dimostrazione:
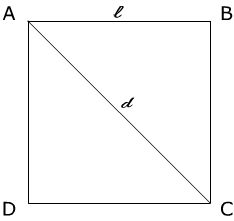
Hai visto cosa abbiamo scritto sopra? Che le diagonali quadrato dividono la figura in due triangoli rettangoli uguali tra loro. Ci basta quindi calcolare la prima diagonale per ottenere anche la seconda. Ragioniamo cioè su un triangolo rettangolo isoscele, ovvero che ha i cateti uguali.
Guardando la figura al lato possiamo renderci conto che AD=DC sono i cateti del triangolo ADC, mentre la diagonale del quadrato AC è l’ipotenusa del triangolo.
Possiamo quindi applicare il teorema di Pitagora per il calcolo dell’ipotenusa:
AC2=AD2+DC2
Chiamando la diagonale del quadrato AC=d e i cateti AD=AC=l, allora possiamo scrivere
d2=l2+l2
d2=2l2
d=l√2
Come calcolare la diagonale di un quadrato
All’interno dei vari esercizi, possono sostanzialmente capitare 2 diversi casi. Per sfruttare la formula appena vista abbiamo sempre bisogno del lato. Vediamo come risolvere:
- Come calcolare la diagonale del quadrato avendo l’area
In questo caso si parte dall’area. Per calcolare il lato si usa la formula inversa di A=l2, cioè l=√A basta fare la radice quadrata dell’area per ottenere il lato. A questo punto per calcolare la diagonale del quadrato basta moltiplicare per la radice di 2. - Come calcolare la diagonale del quadrato noto il perimetro
Il caso è analogo al precedente ma si parte noto il perimetro. La formula da usare è quindi P=4l e per trovare il lato usiamo la formula inversa l=P/4. Ci basta quindi dividere il perimetro per 4 per ottenere il lato. A questo punto moltiplichiamo per la radice quadrata di 2 e abbiamo ottenuto la diagonale.
Come calcolare il lato di un quadrato conoscendo la diagonale
La richiesta è molto semplice e basta davvero fare un solo passaggio. E’ sufficiente applicare l’inversa della formula diagonale quadrato. Cioè:
d=l√2 → d/√2=l → l=(d√2)2
Quindi data la diagonale di un quadrato, per calcolare il lato mi basta moltiplicare la diagonale per radice quadrata di 2 e poi dividere il risultato per 2.
Esempio
Calcola perimetro e area del quadrato con diagonale 32 cm.
L’anello di congiunzione, come abbiamo già detto, tra la diagonale di quadrato e il suo perimetro e l’area, è proprio il calcolo del lato. Applichiamo subito quindi la formula inversa della diagonale:
l=(d√2)2
l=(32√2)/2 = 22,63 cm
A questo punto possiamo calcolare il perimetro e l’area con le loro formule:
p=4l =4·22,63 = 90,51 cm
A=l2 = 22.632= 512,12 cm2
Non dimenticare mai di inserire le unità di misura quando svolti i vari calcoli.
Suggerimenti e consigli
Troverai su internet diversi siti che ti mostrano varie formule per calcolare direttamente le diagonali quadrato partendo dall’area e dal perimetro. Noi ti consigliamo di imparare solo la relazione che lega diagonale e lato. Poi procedi con i ragionamenti che ti abbiamo indicato. Risparmierai energie mentali e correrai meno il rischio di commettere errori mnemonici. E’ meglio imparare 1 formula piuttosto che doverne ricordare poi 3!