La formula di Erone è uno dei metodi meno conosciuti per calcolare l’area di un triangolo generico note le misure dei tre lati.
Dato un triangolo i cui lati misurano a, b, c, il cui semiperimetro vale p, allora l’area si può calcolare come:
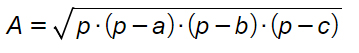
Enunciato e definizione
L’area di un triangolo generico è pari alla radice quadrata del semiperimetro per la differenza tra semiperimetro meno il primo lato, moltiplicato per la differenza tra semiperimetro meno il secondo lato, moltiplicato la differenza tra semiperimetro e terzo lato.
Osservazioni:
Come si nota dall’enunciato, nella formula di Erone sono presenti le misure dei tre lati del triangolo generico e la misura del semi-perimetro. Questo significa che, volendo calcolare l’area di un triangolo con la formula di Erone, serve il perimetro (da dividere per 2) e tutti i lati noti.
Come applicare la formula di Erone
Immaginiamo di conoscere tutti e tre i lati di un triangolo. Se si trattasse di un triangolo rettangolo potremmo calcolare l’area sfruttando la formula cateto maggiore per cateto minore diviso due. Ma se il triangolo è scaleno l’unica formula utilizzabile è base per altezza diviso due. Per calcolare l’altezza possono essere necessari tanti calcoli non sempre semplici per cui può essere utile e rapido applicare la formula di Erone.
Alcuni problemi con la formula di Erone
Esercizio 1
Calcolare l’area di un triangolo scaleno con i lati di dimensioni pari a 2cm, 3cm e 4cm.
Svolgimento
Iniziamo calcolando il perimetro, poi il semiperimetro, del triangolo. Essendo i numeri molto semplici possiamo scrivere
2p=a+b+c=2+3+4=9cm
p=9/2=4,5 cm
Posso già procedere con l’applicazione della Formula di Erone, andando a sostituire i dati:
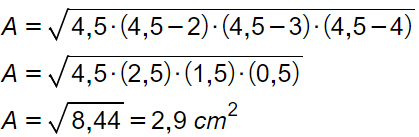
Esercizio 2
I lati di un triangolo misurano 10, 12 e 15 cm. Calcolare la misura dell’area del triangolo e del cerchio inscritto.
Svolgimento
Possiamo applicare direttamente la formula di Erone al triangolo dopo aver calcolato il semiperimetro.
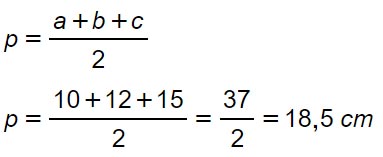
Di seguito applichiamo la formula dell’area:

Formula di Erone dimostrazione
La dimostrazione della formula di Erone è un po’ lunga e laboriosa. Per cui cerchiamo di vederla semplificando al massimo i vari passaggi.
Disegniamo innanzitutto un triangolo scaleno di lati a, b, c e tracciamo l’altezza h relativa alla base c.
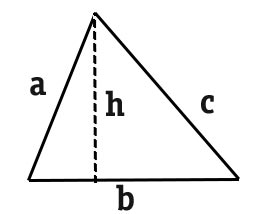
La base b resta divisa in due parti x e (b-x). Per calcolare quanto vale x, applichiamo il teorema di Pitagora ai due triangoli rettangoli.
Per i due triangoli vale la relazione:
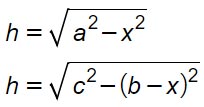
Uguagliamo le due misure, dato che si tratta della stessa altezza, per poter così calcolare il valore dell’incognita x.
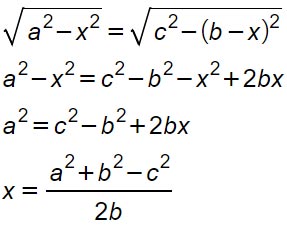
Una volta trovata l’incognita x, possiamo sostituirla nella formula dell’altezza.
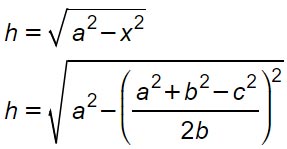
Per cui possiamo calcolare l’area del triangolo scaleno usando la formula classica: base per altezza diviso 2.
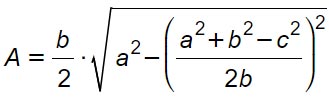
In alcuni libri questa che abbiamo trovato viene presentata come una prima formula di Erone. Tuttavia risulta abbastanza difficile da ricordare per cui sono necessarie alcuni passaggi algebrici per renderla più semplice.
Il prossimo passaggio è quello di portare tutto all’interno della radice:
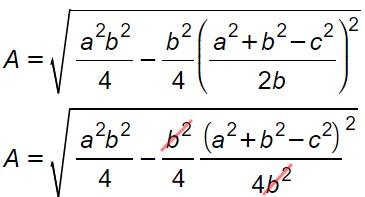
Una volta effettuata la semplificazione in rosso, otteniamo:
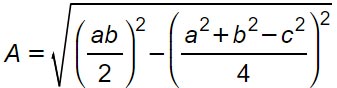
Ti ricordi che nei prodotti notevoli abbiamo parlato di differenza di quadrati? Eseguendo la scomposizione otteniamo:
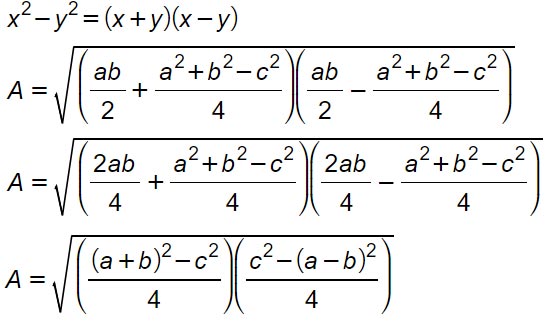
Nell’ultimo passaggio abbiamo scomposto i termini in parentesi in quadrati di binomio. Ora, ripetiamo la scomposizione della differenza di quadrati.
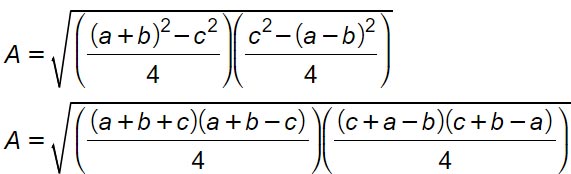
Ora possiamo considerare a+b-c come a+b+c-2c così che la somma dei primi tre sia il perimetro. Stacchiamo inoltre le varie parentesi per ottenere 4 prodotti.
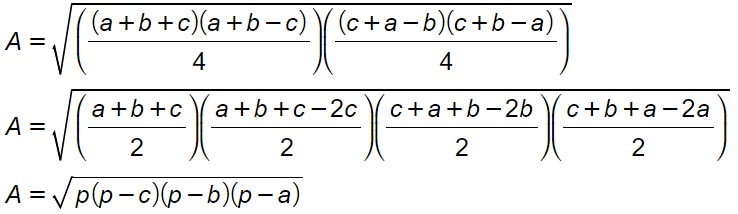
Dove (a+b+c)/2 è il semiperimetro p del triangolo. In questo modo abbiamo così completato la dimostrazione della formula di Erone.
Conclusioni
La formula di Erone può essere utile nello svolgimento di alcuni problemi di geometria per il calcolo dell’area di un triangolo generico. In genere si preferiscono altre formule, per rendere il calcolo meno numerico, ma va tenuta presente come un’utile alternativa.
Hai trovato le risposte che cercavi con questa lezione? Hai risolto i tuoi dubbi? Lascia un commento in basso, ci aiuterai a rendere più completi gli appunti e le dispense che ogni giorni ti offriamo gratuitamente.
la formula di Erone consente di individuare se le misure dei lati di un triangolo ,che sembra retto graficamente, lo è o non lo è;(in mancanza di un compasso che circoscriva il triangolo in questione)
ho constatato che se il rapporto fra area e perimetro è =1/2, allora si tratta di un triangolo costruito con la terna Pitagorica 3-4-5;
Se la terna ha valori doppi( 6-8-10) allora il rapporto fra area e perimetro è =1(uno).
Se il triangolo scaleno(ottuso) ha due lati uguali al raggio del cerchio in cui è inscritto allora :
il lato maggiore vale 1,6r;
e ,la sua area è la metà del triangolo retto con ipotenusa coincidente con il diametro; in questa configurazione il rapporto fra Area e perimetro è=2/3,
li, 20 maggio 2019
Calcola l’area del triangolo con la forma di Erone i lati hanno queste misure A3 cm B 2 cm C 1 cm Grazie buon divertimento
Un divertente quesito. Possiamo dare piccolo suggerimento ai nostri lettori. Cercate che cos’è la disuguaglianza triangolare 😉
Ho ricevuto in gioventù (aimè lontana) una lezione da un mio principale (laurea in chimica) circa la misurazione di una terrazza da asfaltare, usando strumenti rudimentali (cordella metrica). Datala forma irregolare il metodo più celere e affidabile è risultato essere la suddivisione in tanti triangoli sia pure irregolari, dato che il triangolo è la figura indefoformabile per eccellenza. Da allora (40 anni fa) non me lo sono più scordato il Teorema di Erone, nonostante all’esame di diploma fossimo tutti ben preparati 8per merito di un ingegnere, capacissimo esigentissimo e finto burbero. ma Erone proprio non me lo ricordavo.
–recentemente mi sono imbattuto nel quesito se Erone fosse pervenuto alla sua formula nel modo seguente e poi l’ha nascosta con un poi’ di algebra: si tratta del triangolo retto 3-4-5 di Pitagora che ha tre tangenti al cerchio inscritto che valgono rispettivamente 1-2-3 che sostituite nella sua formula offrono il seguente risultato quando si indica il lato a=(n+2) ; b=(n+3) ; c=(n+4 ) ove n=1.
A=√ [(p(p-a)(p-b)(p-c)] = √6(6-5)(6-4)(6-3)= dove 1 2 e 3 sono le tre tangenti geometriche del triangolo pitagorico rispetto al cerchio inscritto, che offre A= √6(1*2*3)=√ 6(6)=√36 (u)^4 = 6 (u)^2.
Quindi avremmo scoperto come Erone avesse trovato la formula verosimilmente.
Calcoliamo ora in modo tradizionale A= (a*b)/2= (n+2)(n+3)/2 ovvero 2A= (n^2+5n+6) che è la funzione che genera l’area del rettangolo in cui è inscritto il triangolo.
Quindi risolviamo la parabola ed otteniamo le due radici x ‛=(-5 (u)) dove (u) indica l’unità di misura, che è somma dei due coefficiente di X ed x‟= 6(u^2) che è coefficiente C della parabola .
E qui si osserva che se abbiamo disegnato il triangolo correttamente possiamo spiegare anche il significato dei segni positivi e negativi.
Nel caso concreto il triangolo inscritto nel cerchi grande di raggio c/2=2,5,ha i cateti (a)parallelo all’asse X e il cateto( b)parallelo all’asse Y di simmetria. Il cateto c=5 ha invece pendenza negativa e di conseguenza ha due tangenti geometriche negative( -2 e -3) il cui prodotto =A=6 (u^2)
Infine,segnalo che il coefficiente 1/2 nella formula dell’area del triangolo ha significato di cos𝝿/3= 1/2
= (cos60)=1/2°,dove 60= (𝞪+𝛃+𝛄)/3=180°/3
pertanto notiamo che l’area dipende sempre da una funzione angolare del cerchio e ne abbiamo conferma anche nel teorema di Carnot/Kashj. detto teorema del coseno.
li, 20/2/24
Saluti da (Joseph) pitagorico.