Disequazioni Irrazionali – le formule e le regole per risolverle

Le disequazioni irrazionali sono delle disequazioni in cui compare il simbolo della radice. Generalmente mettono in difficoltà gli studenti, nonostante la loro risoluzione possa essere eseguita con poche semplici regole. In questa lezione vedremo come si risolvono le disequazioni irrazionali e quali sono le formule da usare per arrivare alla soluzione senza il rischio di sbagliare.

Nella prima parte vedremo quali sono le formule per risolvere le disequazioni irrazionali, mentre dedicheremo un’ampia seconda parte agli esercizi svolti e agli esempi. Ti consigliamo quindi di leggere con calma questa lezione perché troverai tutti i passaggi con commento e spiegazione.

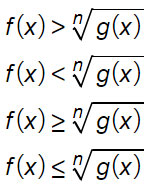
f(x) e g(x) sono due generici polinomi e il secondo di questi compare sotto il segno della radice, che può essere di indice dispari (il caso più semplice da risolvere) o pari. Per il caso minore (e minore uguale) e per il caso maggiore (e maggiore uguale) esistono due metodi o meglio due formule risolutive differenti.

Tabella per risolvere disequazioni irrazionali

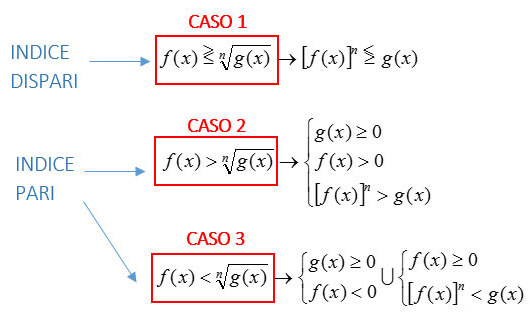
In questo piccolo schema sono presenti le formule sulle disequazioni irrazionali che andrai ad utilizzare per risolvere gli esercizi. Vediamo ora nel dettaglio ogni singolo caso.

Disequazioni irrazionali ad indice dispari

E’ il CASO 1 nelle formule che hai visto in alto. Si tratta del caso più semplice visto che è sufficiente elevare solo all’n-esima potenza entrambi i membri della disequazione. In questo modo riusciamo a far sparire i radicali dall’esercizio. Non importa che la disequazione irrazionale abbia il maggiore o il minore o l’uguale, in ogni caso il procedimento è sempre lo stesso.

Esempio

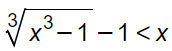
Isoliamo il radicale al primo membro ed eleviamo alla terza potenza entrambi i membri. Facendo il cubo di binomio, si ottiene quindi:

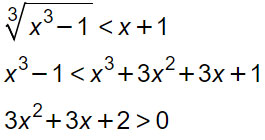
Abbiamo ottenuto a questo punto una disequazione di secondo grado che risolviamo con la formula del delta. Poiché:

Δ=9-24<0 → la soluzione è verificata ∀x∈R (infatti tutti i termini sono positivi per cui sarà certamente maggiore di 0)

Disequazioni irrazionali ad indice pari

Se l’indice del radicale è pari dobbiamo distinguere due diversi casi e procedere in maniera differente a seconda del verso della disequazione.

1 – CASO 2

Quello che abbiamo nelle formule generali definito come caso due vede la presenza del segno maggiore (o maggiore e uguale).

In questa circostanza, oltre alla condizione di esistenza del radicale g(x) maggiore e uguale di 0, deve valere f(x)>0 poiché se g è maggiore di 0 ed f è maggiore di g, allora anche f sarà maggiore di 0. E’ così necessario risolvere il sistema di disequazioni.

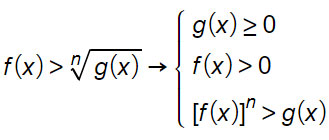
Esempio

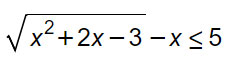
La disequazione irrazionale può essere scritta nella forma:

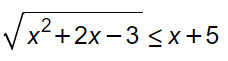
Per la realtà del radicale deve essere x²+2x-3≥0

Inoltre il secondo membro x+5 non deve essere negativo perché maggiore o uguale al primo membro, che non è certamente negativo visto che è il risultato di un radicale. In tali ipotesi si possono elevare al quadrato entrambi i membri, per cui si ha:

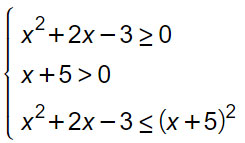
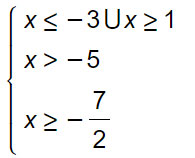
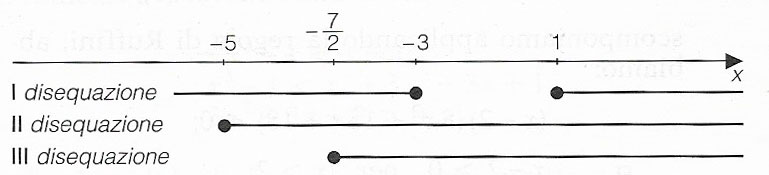
Dall’esame della figura si deduce che il sistema e quindi anche la disequazione irrazionale della traccia sono verificati per:

-7/2 ≤ x ≤-3 ∪ x ≥1

2 – CASO 3

Nella disequazioni con i radicali compare stavolta il segno minore. In questo caso è necessario risolvere attraverso l’unione di due sistemi di disequazioni:

Infatti se f(x) è negativo la disequazione di partenza è sicuramente verificata, dato che il radicale è certamente maggiore di un numero negativo. Se f(x) è maggiore o uguale di zero, invece, la disequazione irrazionale è verificata elevando alla potenza n-esima.

Esempio

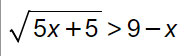
La disequazione irrazionale ad indice pari è equivalente all’unione dei due seguenti sistemi.

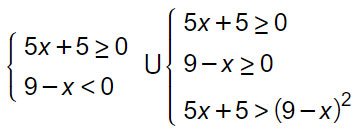
Se il secondo membro della disequazione data è negativo, essa è verificata. Se non è negativo eleviamo al quadrato entrambi i membri per risolvere.

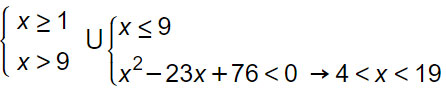
La disequazione 5x+5≥0 nel secondo sistema può essere tralasciata perché implicita nella disequazione 5x+5>(9-x)². Per questa ragione otteniamo come risultato:

x>9 ∪ 4<x≤9

Mettendo questi risultati otteniamo che la disequazione irrazionale è verificata per x>4.

Esercizi svolti

1. Il primo degli esempi che ti proponiamo è molto semplice. Abbiamo indice dispari, per cui non sono necessarie condizioni di esistenza, ma è sufficiente elevare al cubo entrambi i membri della disequazione.

2. Il secondo esercizio svolto presenta un trucchetto che fino ad ora non abbiamo ancora visto: la radice va sempre isolata rispetto a tutti gli altri termini. Questo significa che il radicale deve stare da solo o a primo o a secondo membro.

Come puoi vedere nell’ultima disequazione abbiamo svolto un quadrato di binomio per arrivare alla soluzione temporanea. Per ottenere la soluzione dell’esercizio è necessario fare uno studio dello schema grafico.

 Poiché stiamo risolvendo una sistema di disequazioni, bisogna prendere l’intervallo in cui c’è sempre linea continua. Ecco la ragione per cui la soluzione dell’esercizio è: +2<x<+3.

3. Aumentiamo il grado di difficoltà e proviamo a risolvere esercizi con le equazioni irrazionali con due radicali. Vediamo subito la traccia ed iniziamo a risolvere:

La prima operazione è stata quella di portare tutte le radici allo stesso membro e poi scrivere un sistema con le due condizioni di esistenza dei radicali e l’elevazione a potenza. Quest’ultima operazione riesce in genere più difficile agli studenti ma è piuttosto semplice: ogni radicale va considerato come un termine a parte.

Per cui il binomio di cui fare il quadrato è composto da 2 radici. Si fa così il quadrato del primo radicale, il quadrato del secondo radicale e il doppio prodotto, che come risultato mi dà una nuova radice. Poche semplici operazioni algebriche e mi portano al sistema finale.

A questo punto considerando che la condizione di esistenza dell’ultimo radicale ottenuto mi porterebbe alle stesse disequazioni già scritte  nel sistema, dobbiamo solo aggiungere 2-x>0, rispettando il caso 2 della teoria vista sopra.

Tracce di esercizi da risolvere con soluzioni

Il primo esercizio da risolvere sulle disequazioni con i radicali presenta un grado di difficoltà molto simile all’ultimo esempio visto assieme. E’ necessario quindi scrivere un solo sistema con le condizioni di esistenza di tutti i radicali e infine elevare tutto al quadrato. Fai attenzione che ti troverai una nuova disequazione irrazionale con il maggiore, per  cui dovrai rispettare il caso 3 e passare a due sistemi.

In questo esercizio avrai la possibilità di verificare il tuo grado di abilità con le disequazioni irrazionali fratte. Come per le disequazioni razionali fratte anche in questo caso dovrai studiare separatamente numeratore e denominatore imponendo ad entrambe il maggiore di zero. Al numeratore non avrai alcun problema, mentre al denominatore ti troverai a dover risolvere una disequazione irrazionale con il segno maggiore.

Se hai dubbi, incertezze sulla lezione di oggi o se non sai come risolvere i tuoi compiti, contattaci. Il nostro staff è a tua disposizione! Se la lezione ti è stata d’aiuto, lasciaci un feedback e condividi gli appunti con i tuoi compagni… potrà essere un utile risorsa anche per loro!